Advertisements
Advertisements
प्रश्न
Evaluate:
`cos[tan^-1 (3/4)]`
उत्तर
Let `tan^-1 (3/4) = theta`
`3/4` = tan θ
tan θ = `3/4`
∴ cos θ = `4/5`
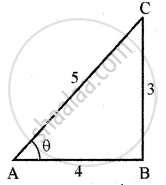
`[because theta = tan^-1 3/4]`
Now `cos[tan^-1 (3/4)] = cos theta = 4/5`
APPEARS IN
संबंधित प्रश्न
Prove that:
`tan^-1 ((sqrt(1 + x) - sqrt(1 - x))/(sqrt(1 + x) + sqrt(1 - x))) = pi/4 - 1/2 cos^-1 x`, for `- 1/sqrt2 <= x <= 1`
[Hint: put x = cos 2θ]
`sin^-1 1/2-2sin^-1 1/sqrt2`
In ΔABC, if a = 18, b = 24, c = 30 then find the values of sinA
lf `sqrt3costheta + sintheta = sqrt2`, then the general value of θ is ______
The value of cot (- 1110°) is equal to ______.
If sin-1 x – cos-1 x `= pi/6,` then x = ____________.
Which of the following functions is inverse of itself?
`tan^-1 (1 - x)/(1 + x) = 1/2tan^-1x, (x > 0)`, x then will be equal to.
`2tan^-1 (cos x) = tan^-1 (2"cosec" x)`, then 'x' will be equal to
Assertion (A): The domain of the function sec–12x is `(-∞, - 1/2] ∪ pi/2, ∞)`
Reason (R): sec–1(–2) = `- pi/4`
