Advertisements
Advertisements
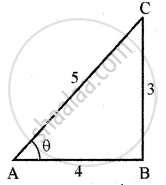
प्रश्न
Evaluate:
`cos[tan^-1 (3/4)]`
उत्तर
Let `tan^-1 (3/4) = theta`
`3/4` = tan θ
tan θ = `3/4`
∴ cos θ = `4/5`
`[because theta = tan^-1 3/4]`
Now `cos[tan^-1 (3/4)] = cos theta = 4/5`
APPEARS IN
संबंधित प्रश्न
Find the domain of the following function:
`f(x)=sin^-1x^2`
Evaluate the following:
`tan^-1 1+cos^-1 (-1/2)+sin^-1(-1/2)`
Evaluate cot(tan−1(2x) + cot−1(2x))
Solve: tan-1 (x + 1) + tan-1 (x – 1) = `tan^-1 (4/7)`
If 2tan-1 (cos x) = tan-1 (cosec2 x), then x = ______.
Prove that `cot(pi/4 - 2cot^-1 3)` = 7
`"sin"^-1 (1/sqrt2)`
`sin[π/3 - sin^-1 (-1/2)]` is equal to:
Number of values of x satisfying the system of equations `sin^-1sqrt(2 + e^(-2x) - 2e^-x) + sec^-1sqrt(1 - x^2 + x^4) = π/2` and `5^(1+tan^-1x)` = 4 + [cos–1x] is ______ (where [.] denotes greatest integer function)
sin [cot–1 (cos (tan–1 x))] = ______.
