Advertisements
Advertisements
Question
Evaluate:
`cos[tan^-1 (3/4)]`
Solution
Let `tan^-1 (3/4) = theta`
`3/4` = tan θ
tan θ = `3/4`
∴ cos θ = `4/5`
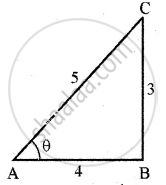
`[because theta = tan^-1 3/4]`
Now `cos[tan^-1 (3/4)] = cos theta = 4/5`
APPEARS IN
RELATED QUESTIONS
Prove that:
`tan^-1 ((sqrt(1 + x) - sqrt(1 - x))/(sqrt(1 + x) + sqrt(1 - x))) = pi/4 - 1/2 cos^-1 x`, for `- 1/sqrt2 <= x <= 1`
[Hint: put x = cos 2θ]
`sin^-1{cos(sin^-1 sqrt3/2)}`
Evaluate the following:
`cot^-1 1/sqrt3-\text(cosec)^-1(-2)+sec^-1(2/sqrt3)`
In ΔABC, if a = 18, b = 24, c = 30 then find the values of tan `A/2`
Evaluate cot(tan−1(2x) + cot−1(2x))
Find the principal value of cosec–1(– 1)
The domain of the function defined by f(x) = sin–1x + cosx is ______.
The equation tan–1x – cot–1x = `(1/sqrt(3))` has ______.
If 2 tan–1 (cosx) = tan–1 (2 cosec x), then sin x + cos x is equal to ______.
Find the value of `tan^-1(x/y) + tan^-1((y - x)/(y + x))`
