Advertisements
Advertisements
प्रश्न
Find the roots of the following quadratic equations (if they exist) by the method of completing the square.
`x^2-4sqrt2x+6=0`
उत्तर
We have been given that,
`x^2-4sqrt2x+6=0`
Now we take the constant term to the right hand side and we get
`x^2-4sqrt2x=-6`
Now add square of half of co-efficient of ‘x’ on both the sides. We have,
`x^2 - 4sqrt2x+(2sqrt2)^2=(2sqrt2)^2-6`
`x^2+(2sqrt2)^2-2(2sqrt2)x=2`
`(x-2sqrt2)^2=2`
Since right hand side is a positive number, the roots of the equation exist.
So, now take the square root on both the sides and we get
`x-2sqrt2=+-sqrt2`
`x=2sqrt2+-sqrt2`
Now, we have the values of ‘x’ as
`x=2sqrt2+sqrt2=3sqrt2`
Also we have,
`x=2sqrt2-sqrt2=sqrt2`
Therefore the roots of the equation are `3sqrt2` and `sqrt2`.
APPEARS IN
संबंधित प्रश्न
Solve the following quadratic equation by completing square method : x2 + 10x + 21 = 0.
Find the roots of the quadratic equations 2x2 + x + 4 = 0 by applying the quadratic formula.
`5x^2-6x-2=0`
A farmer prepares rectangular vegetable garden of area 180 sq meters. With 39 meters of barbed wire, he can fence the three sides of the garden, leaving one of the longer sides unfenced. Find the dimensions of the garden.
Solve the following quadratic equation by completing the square method.
x2 + 2x – 5 = 0
Fill in the gaps and complete.
If α, β are roots of quadratic equation,
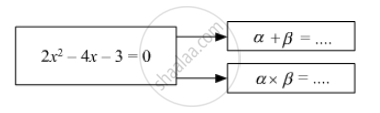
Find the value of discriminant.
`sqrt2x^2 + 4x + 2sqrt2 = 0`
Determine the nature of roots of the following quadratic equation.
x2 – 4x + 4 = 0
Sum of the area of two squares is 400 cm2. If the difference of their perimeters is 16 cm, find the sides of two squares.
For solving the quadratic equations `"x"^2 + 8"x" =-15` by completing the square method, find the third term.
