Advertisements
Advertisements
प्रश्न
Find the area of the following fields. All dimensions are in metres.
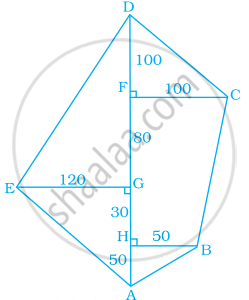
उत्तर
Area of the given figure
= Area of ΔDCF + Area of ΔEGD + Area of trapezium FCBH + Area of ΔEGA + Area of ΔAHB
∴ Area of ΔDCF = `1/2` × Base × Height
= `1/2 xx 100 xx 100`
= `10000/2`
= 5000 m2
Area of ΔEGD = `1/2` × Base × Height
= `1/2 xx 120 xx 180`
= 60 × 180
= 10800 m2
Area of trapezium = `1/2` × [Sum of parallel sides] × Height
= `1/2 xx [100 + 50] xx 110`
= `1/2 xx 150 xx 110`
= 75 × 110
= 8250 m2
Area of ΔEGA = `1/2` × Base × Height
= `1/2 xx 120 xx 80`
= 60 × 80
= 4800 m2
Area of ΔAHB = `1/2` × Base × Height
= `1/2 xx 50 xx 50`
= 25 × 50
= 1250 m2
Thus, the area of the complete figure
= 5000 + 10800 + 8250 + 4800 + 1250
= 30100 m2
APPEARS IN
संबंधित प्रश्न
The area of a trapezium is 34 cm2 and the length of one of the parallel sides is 10 cm and its height is 4 cm. Find the length of the other parallel side.
Find the altitude of a trapezium whose area is 65 cm2 and whose bases are 13 cm and 26 cm.
Find the sum of the lengths of the bases of a trapezium whose area is 4.2 m2 and whose height is 280 cm.
Find the area of a trapezium whose parallel sides of lengths 10 cm and 15 cm are at a distance of 6 cm from each other. Calculate this area as the difference of the area of a rectangle and the sum of the areas of two triangles.
The area of a trapezium is 1586 cm2 and the distance between the parallel sides is 26 cm. If one of the parallel sides is 38 cm, find the other.
☐ PQRS is an isosceles trapezium l(PQ) = 7 cm. seg PM ⊥ seg SR, l(SM) = 3 cm, Distance between two parallel sides is 4 cm, find the area of ☐ PQRS.
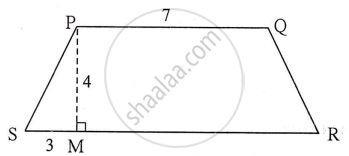
Find the missing values.
| Height 'h' | Parallel side 'a` | Parallel side 'b` | Area |
| 10 m | 12 m | 20 m |
The sunshade of a window is in the form of isosceles trapezium whose parallel sides are 81 cm and 64 cm and the distance between them is 6 cm. Find the cost of painting the surface at the rate of ₹ 2 per sq.cm
In a trapezium if the sum of the parallel sides is 10 cm and the area is 140 sq.cm, then the height is
The areas of two circles are in the ratio 49 : 64. Find the ratio of their circumferences.
