Advertisements
Advertisements
प्रश्न
Find the left and right limits of f(x) = `(x^2 - 4)/((x^2 + 4x+ 4)(x + 3))` at x = – 2
उत्तर
f(x) = `(x^2 - 4)/((x^2 + 4x+ 4)(x + 3))` at x = – 2
f(x) = `((x + 2)(x - 2))/((x + 2)^2 (x + 3))`
f(x) = `(x - 2)/((x +2)(x +3))`
o find the let imit of f(x) at x = – 2
Put x = – 2 – h
Where h > 0
When x → – 2
We have h → 0
`lim_(x -> - 2^-) f(x) = lim_("h" -> 0) ((-2 - "h")- 2)/((-2 "h" + 2)(- 2 - "h" + 3)`
= `lim_("h" -> 0) (-4 - "h")/((- "h")(1 - "h"))`
=`lim_("h" -> 0) 1/"h" ((4 + "h")/(1 - "h"))`
= `1/0 ((4 + 0)/(1 - 0))`
= `oo`
`lim_(x -> - 2^-) f(x) = oo`
o find the right limit of f(x) at x = – 2
Put x = – 2 + h
Where h > 0
When x → – 2
We have h → 0
`lim_(x -> - 2) f(x) = lim_("h" -> 0) ((-2 + "h") - 2)/((-2 + "h" + 2)(-2 + "h" + 3))`
= `lim_("h" -> 0) (-4 + "h")/("h"(1 + "h"))`
= `lim_("h" -> 0) 1/"h"(("h" - 4)/(1 +"h"))`
= `1/0 ((0 - 4)/(1 + 0))`
= `- oo`
`lim_(x -> - 2^-) f(x) = - oo`
APPEARS IN
संबंधित प्रश्न
Evaluate the following limit:
`lim_(x -> 2)[(x^(-3) - 2^(-3))/(x - 2)]`
Evaluate the following limit:
If `lim_(x -> 1)[(x^4 - 1)/(x - 1)]` = `lim_(x -> "a")[(x^3 - "a"^3)/(x - "a")]`, find all possible values of a
In the following example, given ∈ > 0, find a δ > 0 such that whenever, |x – a| < δ, we must have |f(x) – l| < ∈.
`lim_(x -> 2) (x^2 - 1)` = 3
Evaluate the following :
Given that 7x ≤ f(x) ≤ 3x2 – 6 for all x. Determine the value of `lim_(x -> 3) "f"(x)`
In problems 1 – 6, using the table estimate the value of the limit
`lim_(x -> 0) (sqrt(x + 3) - sqrt(3))/x`
| x | – 0.1 | – 0.01 | – 0.001 | 0.001 | 0.01 | 0.1 |
| f(x) | 0.2911 | 0.2891 | 0.2886 | 0.2886 | 0.2885 | 0.28631 |
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> x/2) tan x`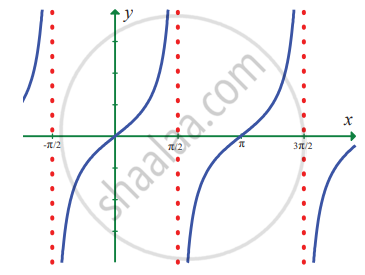
If f(2) = 4, can you conclude anything about the limit of f(x) as x approaches 2?
Evaluate the following limits:
`lim_(x - 0) (sqrt(1 + x^2) - 1)/x`
Evaluate the following limits:
`lim_(x -> oo) (x^4 - 5x)/(x^2 - 3x + 1)`
Evaluate the following limits:
`lim_(x -> oo) ((2x^2 + 3)/(2x^2 + 5))^(8x^2 + 3)`
Evaluate the following limits:
`lim_(x -> 0) (2 "arc"sinx)/(3x)`
Evaluate the following limits:
`lim_(x -> 0) (2^x - 3^x)/x`
Evaluate the following limits:
`lim_(x -> 0) (sqrt(1 + sinx) - sqrt(1 - sinx))/tanx`
Choose the correct alternative:
`lim_(x -> oo) sinx/x`
Choose the correct alternative:
`lim_(x -> oo) ((x^2 + 5x + 3)/(x^2 + x + 3))^x` is
Choose the correct alternative:
If `lim_(x -> 0) (sin "p"x)/(tan 3x)` = 4, then the value of p is
If `lim_(x->1)(x^5-1)/(x-1)=lim_(x->k)(x^4-k^4)/(x^3-k^3),` then k = ______.
`lim_(x→-1) (x^3 - 2x - 1)/(x^5 - 2x - 1)` = ______.
