Advertisements
Advertisements
प्रश्न
In problems 1 – 6, using the table estimate the value of the limit
`lim_(x -> 0) (sqrt(x + 3) - sqrt(3))/x`
| x | – 0.1 | – 0.01 | – 0.001 | 0.001 | 0.01 | 0.1 |
| f(x) | 0.2911 | 0.2891 | 0.2886 | 0.2886 | 0.2885 | 0.28631 |
उत्तर
Let f(x) = `lim_(x -> 0) (sqrt(x + 3) - sqrt(3))/x`
| x | – 0.1 | – 0.01 | – 0.001 | 0.001 | 0.01 | 0.1 |
| f(x) |
`(sqrt(3 - 0.1) - sqrt(3))/(- 0.1)` = `(1.703 - 1.732)/(- 0.1)` = 0.29 |
`(sqrt(3 - 00.1) - sqrt(3))/(- 0.01)` = `(1.703 - 1.732)/(- 0.01)` = 0.288 |
`(sqrt(3 - 0.001) - sqrt(3))/(- 0.001)` = `(0.000284)/(- 0.001)` = 0.288 |
`(sqrt(3 + 0.001) - sqrt(3))/(- 0.001)` = `(0.000289)/(0.001)` = 0.289 |
`(sqrt(3 + 0.01) - sqrt(3))/(0.01)` = `(0.00288)/(0.01)` = 0.288 |
`(sqrt(3 + 0.1) - sqrt(3))/(0.1)` = `(0.0286)/(0.1)` = 0.286 |
`lim_(x -> 0) (sqrt(x + 3) - sqrt(3))/x` = 0.288
APPEARS IN
संबंधित प्रश्न
Evaluate the following limit:
`lim_(x -> 3)[sqrt(2x + 6)/x]`
Evaluate the following limit :
`lim_(x -> 1)[(x + x^2 + x^3 + ......... + x^"n" - "n")/(x - 1)]`
Evaluate the following limit :
`lim_(x -> 0)[(root(3)(1 + x) - sqrt(1 + x))/x]`
Evaluate the following :
`lim_(x -> 1) [(x + 3x^2 + 5x^3 + ... + (2"n" - 1)x^"n" - "n"^2)/(x - 1)]`
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 3) (4 - x)`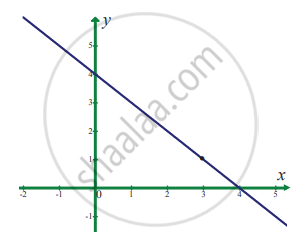
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 1) sin pi x`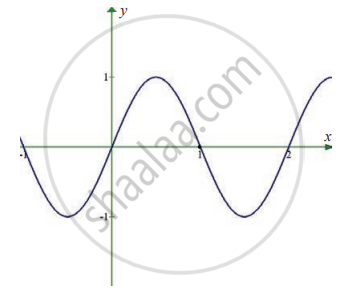
Evaluate the following limits:
`lim_(sqrt(x) -> 3) (x^2 - 81)/(sqrt(x) - 3)`
Show that `lim_("n" -> oo) 1/1.2 + 1/2.3 + 1/3.4 + ... + 1/("n"("n" + 1))` = 1
A tank contains 5000 litres of pure water. Brine (very salty water) that contains 30 grams of salt per litre of water is pumped into the tank at a rate of 25 litres per minute. The concentration of salt water after t minutes (in grams per litre) is C(t) = `(30"t")/(200 + "t")`. What happens to the concentration as t → ∞?
Evaluate the following limits:
`lim_(x -> oo)(1 + "k"/x)^("m"/x)`
Evaluate the following limits:
`lim_(alpha -> 0) (sin(alpha^"n"))/(sin alpha)^"m"`
Evaluate the following limits:
`lim_(x -> 0) ("e"^x - "e"^(-x))/sinx`
Evaluate the following limits:
`lim_(x -> 0) (tan x - sin x)/x^3`
Choose the correct alternative:
`lim_(x -> 0) ("a"^x - "b"^x)/x` =
Choose the correct alternative:
If `f(x) = x(- 1)^([1/x])`, x ≤ 0, then the value of `lim_(x -> 0) f(x)` is equal to
Choose the correct alternative:
If `lim_(x -> 0) (sin "p"x)/(tan 3x)` = 4, then the value of p is
Choose the correct alternative:
`lim_(x -> oo) (1/"n"^2 + 2/"n"^2 + 3/"n"^2 + ... + "n"/"n"^2)` is
`lim_(x -> 0) (sin 4x + sin 2x)/(sin5x - sin3x)` = ______.
