Advertisements
Advertisements
प्रश्न
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 1) sin pi x`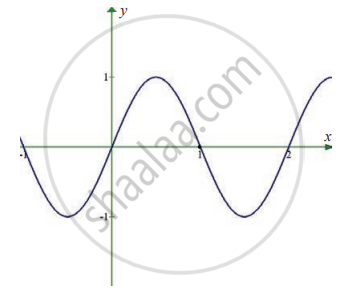
उत्तर
`lim_(x -> 1) sin pi x`
From the graph x = 1, the curve y = f(x) intersects the line x = 1 at x – axis.
∴ y = f(1) = 0
Hence `lim_(x -> 1) sin pix` = 0
APPEARS IN
संबंधित प्रश्न
Evaluate the following limit :
`lim_(x -> 1)[(x + x^2 + x^3 + ......... + x^"n" - "n")/(x - 1)]`
Evaluate the following :
Given that 7x ≤ f(x) ≤ 3x2 – 6 for all x. Determine the value of `lim_(x -> 3) "f"(x)`
Evaluate the following :
`lim_(x -> 0) {1/x^12 [1 - cos(x^2/2) - cos(x^4/4) + cos(x^2/2) cos(x^4/4)]}`
In problems 1 – 6, using the table estimate the value of the limit
`lim_(x -> 0) sin x/x`
| x | – 0.1 | – 0.01 | – 0.001 | 0.001 | 0.01 | 0.1 |
| f(x) | 0.99833 | 0.99998 | 0.99999 | 0.99999 | 0.99998 | 0.99833 |
Sketch the graph of f, then identify the values of x0 for which `lim_(x -> x_0)` f(x) exists.
f(x) = `{{:(sin x",", x < 0),(1 - cos x",", 0 ≤ x ≤ pi),(cos x",", x > pi):}`
Write a brief description of the meaning of the notation `lim_(x -> 8) f(x)` = 25
Evaluate the following limits:
`lim_(x -> 2) (2 - sqrt(x + 2))/(root(3)(2) - root(3)(4 - x))`
Evaluate the following limits:
`lim_(x -> 3) (x^2 - 9)/(x^2(x^2 - 6x + 9))`
Evaluate the following limits:
`lim_(x -> oo) ((2x^2 + 3)/(2x^2 + 5))^(8x^2 + 3)`
Evaluate the following limits:
`lim_(x -> 0) (sin^3(x/2))/x^2`
Evaluate the following limits:
`lim_(x -> 0) (2 "arc"sinx)/(3x)`
Evaluate the following limits:
`lim_(x -> 0) (1 - cos^2x)/(x sin2x)`
Evaluate the following limits:
`lim_(x -> oo) x [3^(1/x) + 1 - cos(1/x) - "e"^(1/x)]`
Evaluate the following limits:
`lim_(x -> 0) (sqrt(2) - sqrt(1 + cosx))/(sin^2x)`
Evaluate the following limits:
`lim_(x -> 0) ("e"^x - "e"^(-x))/sinx`
Evaluate the following limits:
`lim_(x -> 0) (tan x - sin x)/x^3`
Choose the correct alternative:
`lim_(x - oo) sqrt(x^2 - 1)/(2x + 1)` =
Choose the correct alternative:
`lim_(x -> 0) (x"e"^x - sin x)/x` is
`lim_(x -> 0) ((2 + x)^5 - 2)/((2 + x)^3 - 2)` = ______.
`lim_(x -> 0) (sin 4x + sin 2x)/(sin5x - sin3x)` = ______.
