Advertisements
Advertisements
प्रश्न
Sketch the graph of f, then identify the values of x0 for which
f(x) =
उत्तर
f(x) =
From the figure when x = π, y = f(π) = 2.
The function is not defined at x = π since sin x lies in the interval [– 1, 1]
∴ The given function has limits at all points except at x = π
| x | 0 | 2 | ||||
| f(x) | 1 – cos 0 | 1 – cos π | cos 2π | |||
| f(x) | – 1 | 0 | 1 | 1 – (– 1) = 2 | 0 | 1 |
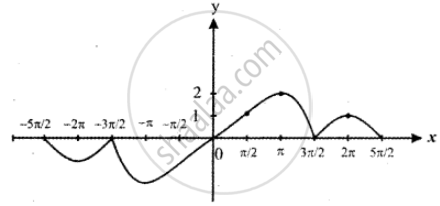
(π, 2) point is not possible since the range of the curve is [– 1, 1] .
Except x0 = π, the curve has limits.
APPEARS IN
संबंधित प्रश्न
Evaluate the following limit:
Evaluate the following limit :
Evaluate the following limit :
In the following example, given ∈ > 0, find a δ > 0 such that whenever, |x – a| < δ, we must have |f(x) – l| < ∈.
Evaluate the following :
Find the limit of the function, if it exists, at x = 1
f(x) =
Evaluate the following :
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
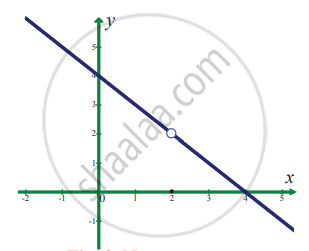
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
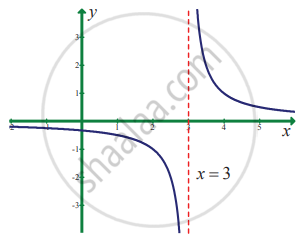
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
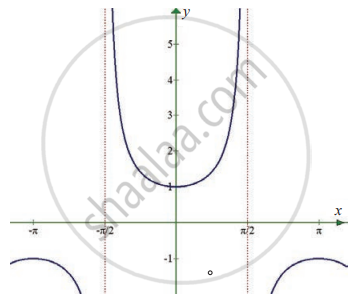
If f(2) = 4, can you conclude anything about the limit of f(x) as x approaches 2?
Evaluate the following limits:
Evaluate the following limits:
Show that
Evaluate the following limits:
Evaluate the following limits:
Evaluate the following limits:
Evaluate the following limits:
Evaluate the following limits:
Choose the correct alternative:
The value of
