Advertisements
Advertisements
प्रश्न
If G is the centroid of a ΔABC, prove that (area of ΔGAB) = (area of ΔGBC) = (area of ΔGCA) = `1/3` (area of ΔABC)
उत्तर
W.K.T the median of a triangle divides it into two triangles of equal area.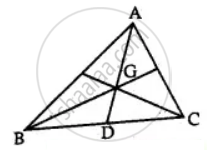
In ΔABC, AD is the median
Area(ΔABD) = Area (ΔACD) ........(1)
In ΔGBC, GD is die median
Area(ΔGBD) = Area (ΔGCD) ........(2)
Sub (2) from (1) we get
Area(ΔABD) – Area (ΔGBD)
= Area(ΔACD) – Area (ΔGCD)
Area(ΔAGB) = Area(ΔAGC) ........(3)
Similarly
Area(ΔAGB) = Area(ΔBGC) ........(4)
From (3) and (4) we get
Area(ΔAGB) = Area(ΔAGC) = Area(ΔBGC) ........(5)
Now
Area(ΔAGB) + Area(ΔAGC) + Area(ΔBGC) = Area(ΔABC)
⇒ Area(ΔAGB) + Area(ΔAGB) + Area(ΔAGB)
= Area(ΔABC) .......(Using 5)
⇒ 3Area(ΔAGB) = Area(ΔABC)
⇒ Area(ΔAGB) = `1/3` area(ΔABC) ........(6)
From (5) and (6) we get
Area(ΔAGB) = Area(ΔAGB) = Area(ΔBGC)
= `1/3` area(ΔABC)
APPEARS IN
संबंधित प्रश्न
Prove by vector method that the median to the base of an isosceles triangle is perpendicular to the base
Prove by vector method that an angle in a semi-circle is a right angle
Prove by vector method that the diagonals of a rhombus bisect each other at right angles
Using vector method, prove that if the diagonals of a parallelogram are equal, then it is a rectangle
Prove by vector method that the area of the quadrilateral ABCD having diagonals AC and BD is `1/2 |bar"AC" xx bar"BD"|`
Prove by vector method that the parallelograms on the same base and between the same parallels are equal in area
Using vector method, prove that cos(α – β) = cos α cos β + sin α sin β
Prove by vector method that sin(α + ß) = sin α cos ß + cos α sin ß
A particle acted on by constant forces `8hat"i" + 2hat"j" - 6hat"k"` and `6hat"i" + 2hat"j" - 2hat"k"` is displaced from the point (1, 2, 3) to the point (5, 4, 1). Find the total work done by the forces
Forces of magnitudes `5sqrt(2)` and `10sqrt(2)` units acting in the directions `3hat"i" + 4hat"j" + 5hat"k"` and `10hat"i" + 6hat"j" - 8hat"k"` respectively, act on a particle which is displaced from the point with position vector `4hat"i" - 3hat"j" - 2hat"k"` to the point with position vector `6hat"i" + hat"j" - 3hat"k"`. Find the work done by the forces
Find the magnitude and direction cosines of the torque of a force represented by `3hat"i" + 4hat"j" - 5hat"k"` about the point with position vector `2hat"i" - 3hat"j" + 4hat"k"` acting through a point whose position vector is `4hat"i" + 2hat"j" - 3hat"k"`
Choose the correct alternative:
If a vector `vecalpha` lies in the plane of `vecbeta` and `vecϒ`, then
Choose the correct alternative:
If `vec"a"*vec"b" = vec"b"*vec"c" = vec"c"*vec"a"` = 0, then the value of `[vec"a", vec"b", vec"c"]` is
Let A, B, C be three points whose position vectors respectively are
`vec"a" = hat"i" + 4hat"j" + 3hat"k"`
`vec"b" = 2hat"i" + αhat"j" + 4hat"k", α ∈ "R"`
`vec"c" = 3hat"i" - 2hat"j" + 5hat"k"`
If α is the smallest positive integer for which `vec"a", vec"b", vec"c"` are noncollinear, then the length of the median, in ΔABC, through A is ______.
Let `veca, vecb, vecc` be three mutually perpendicular vectors of the same magnitude and equally inclined at an angle θ, with the vector `veca + vecb + vecc`. Then, 36 cos22θ is equal to ______.
The value of `[veca + 2vecb - vecc, veca - vecb, veca - vecb - vecc]` is equal to the box product ______.
