Advertisements
Advertisements
प्रश्न
Prove by vector method that the diagonals of a rhombus bisect each other at right angles
उत्तर
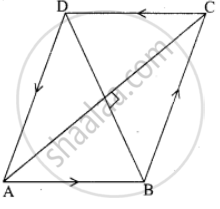
Let ABCD be a rhombus
To prove `bar"AC" * bar"BD"` = 0
We have AB = BC = CD = DA
Now `bar"AC" = bar"AB" + "BC"`
`bar"BD" = bar"BC" + bar"CD"`
= `bar"BC" - bar"AB"` .......`("Since" bar"CD" = - bar"AB")`
`bar"AC" * bar"BD" = (bar"BC" + bar"AB") * (bar"BC" - bar"AB")`
= `(bar"BC")^2 - (bar"AB")^2`
= `("BC")^2 - ("AB")^2`
`bar"AC" * bar"BD"` = 0
∴ `bar"AC"` ⊥' to `bar"BD"`
Hence the result.
APPEARS IN
संबंधित प्रश्न
Prove by vector method that if a line is drawn from the centre of a circle to the midpoint of a chord, then the line is perpendicular to the chord
Prove by vector method that the median to the base of an isosceles triangle is perpendicular to the base
Prove by vector method that an angle in a semi-circle is a right angle
Prove by vector method that the area of the quadrilateral ABCD having diagonals AC and BD is `1/2 |bar"AC" xx bar"BD"|`
Prove by vector method that the parallelograms on the same base and between the same parallels are equal in area
Prove by vector method that sin(α + ß) = sin α cos ß + cos α sin ß
Forces of magnitudes `5sqrt(2)` and `10sqrt(2)` units acting in the directions `3hat"i" + 4hat"j" + 5hat"k"` and `10hat"i" + 6hat"j" - 8hat"k"` respectively, act on a particle which is displaced from the point with position vector `4hat"i" - 3hat"j" - 2hat"k"` to the point with position vector `6hat"i" + hat"j" - 3hat"k"`. Find the work done by the forces
Find the torque of the resultant of the three forces represented by `- 3hat"i" + 6hat"j" - 3hat"k", 4hat"i" - 10hat"j" + 12hat"k"` and `4hat"i" + 7hat"j"` acting at the point with position vector `8hat"i" - 6hat"j" - 4hat"k"` about the point with position vector `18hat"i" + 3hat"j" - 9hat"k"`
Choose the correct alternative:
If `vec"a"*vec"b" = vec"b"*vec"c" = vec"c"*vec"a"` = 0, then the value of `[vec"a", vec"b", vec"c"]` is
Let `veca = αhati + 3hatj - hatk, vecb = 3hati - βhatj + 4hatk` and `vecc = hati + 2hatj - 2hatk` where α, β ∈ R, be three vectors. If the projection of a `veca` on `vecc` is `10/3` and `vecb xx vecc = -6hati + 10hatj + 7hatk`, then the value of α + β is equal to ______.
Let A, B, C be three points whose position vectors respectively are
`vec"a" = hat"i" + 4hat"j" + 3hat"k"`
`vec"b" = 2hat"i" + αhat"j" + 4hat"k", α ∈ "R"`
`vec"c" = 3hat"i" - 2hat"j" + 5hat"k"`
If α is the smallest positive integer for which `vec"a", vec"b", vec"c"` are noncollinear, then the length of the median, in ΔABC, through A is ______.
Let `veca = 2hati + hatj - 2hatk` and `vecb = hati + hatj`. If `vecc` is a vector such that `veca.vecc = |vecc|, |vecc - veca| = 2sqrt(2)`, angle between `(veca xx vecb)` and `vecc` is `π/6`, then the value of `|(veca xx vecb) xx vecc|` is ______.
Let `veca, vecb, vecc` be three mutually perpendicular vectors of the same magnitude and equally inclined at an angle θ, with the vector `veca + vecb + vecc`. Then, 36 cos22θ is equal to ______.
Let `veca, vecb` and `vecc` be three unit vectors such that `|veca - vecb|^2 + |veca - vecc|^2` = 8. Then find the value of `|veca + 2vecb|^2 + |veca + 2vecc|^2`
The value of `[veca + 2vecb - vecc, veca - vecb, veca - vecb - vecc]` is equal to the box product ______.
Let a, b, c ∈ R be such that a2 + b2 + c2 = 1. If `a cos θ = b cos(θ + (2π)/3) = c cos(θ + (4π)/3)`, where θ = `π/9`, then the angle between the vectors `ahati + bhatj + chatk` and `bhati + chatj + ahatk` is ______.
