Advertisements
Advertisements
प्रश्न
In a college, 70% of students pass in Physics, 75% pass in Mathematics and 10% of students fail in both. One student is chosen at random. What is the probability that:
(i) He passes in Physics and Mathematics?
(ii) He passes in Mathematics given that he passes in Physics.
(iii) He passes in Physics given that he passes in Mathematics.
उत्तर
Let x% of students pass in both Physics and Mathematics
Students pass in Physics = 70% ⇒ P (P) = `(70)/(100)`
Students pass in Mathematics = 75% ⇒ P (M) = `(75)/(100)`
Students fail in both = 10%
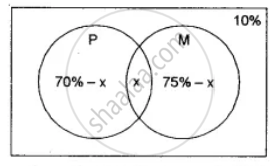
Now students pass in physics only + students pass in mathematics only + students pass in both physics and mathematics = 90%
⇒ 70% - x + x + 75% - x = 90%
x = 55% ⇒ P (M ∩ P) = `(55)/(100)`
(i)
P ( Passes in Physics and Mathematics) = `(55)/(100) = (11)/(20)`
(ii)
P (M/P) = `(P (M ∩ P))/(P(P)`
= `((55)/(100))/(70/(100))`
= `(55)/(70) = (11)/(14)`
(iii)
`P(P/M) = (P(M ∩ P))/(P(M))`
`(55/100)/(75/100)`
= `55/75 = 11/15`
APPEARS IN
संबंधित प्रश्न
A die is thrown three times. Events A and B are defined as below:
A : 5 on the first and 6 on the second throw.
B: 3 or 4 on the third throw.
Find the probability of B, given that A has already occurred.
A bag X contains 4 white balls and 2 black balls, while another bag Y contains 3 white balls and 3 black balls. Two balls are drawn (without replacement) at random from one of the bags and were found to be one white and one black. Find the probability that the balls were drawn from bag Y.
Suppose that 80% of all families own a television set. If 5 families are interviewed at random, find the probability that
a. three families own a television set.
b. at least two families own a television set.
If `P(A) = 6/11, P(B) = 5/11 "and" P(A ∪ B) = 7/11` find
- P(A ∩ B)
- P(A|B)
- P(B|A)
Determine P(E|F).
A coin is tossed three times, where
E: at most two tails, F: at least one tail
Determine P(E|F).
A die is thrown three times,
E: 4 appears on the third toss, F: 6 and 5 appears respectively on first two tosses
A fair die is rolled. Consider events E = {1, 3, 5}, F = {2, 3} and G = {2, 3, 4, 5} Find P (E|F) and P (F|E)
Given that the two numbers appearing on throwing the two dice are different. Find the probability of the event ‘the sum of numbers on the dice is 4’.
A die is tossed thrice. Find the probability of getting an odd number at least once.
A and B are two events such that P (A) ≠ 0. Find P (B|A), if A ∩ B = Φ.
If A and B are events such as that P(A) = `1/2`, P(B) = `1/3` and P(A ∩ B) = `1/4`, then find
1) P(A / B)
2) P(B / A)
A card is drawn from a well-shuffled pack of playing cards. What is the probability that it is either a spade or an ace or both?
Three cards are drawn at random (without replacement) from a well-shuffled pack of 52 playing cards. Find the probability distribution of the number of red cards. Hence, find the mean of the distribution.
Two cards are drawn one after the other from a pack of 52 cards without replacement. What is the probability that both the cards drawn are face cards?
Select the correct option from the given alternatives :
Bag I contains 3 red and 4 black balls while another Bag II contains 5 red and 6 black balls. One ball is drawn at random from one of the bags and it is found to be red. The probability that it was drawn from Bag II
If A and B are two events such that P(A ∪ B) = 0.7, P(A ∩ B) = 0.2, and P(B) = 0.5, then show that A and B are independent
If for two events A and B, P(A) = `3/4`, P(B) = `2/5` and A ∪ B = S (sample space), find the conditional probability P(A/B)
The probability that a car being filled with petrol will also need an oil change is 0.30; the probability that it needs a new oil filter is 0.40; and the probability that both the oil and filter need changing is 0.15. If the oil had to be changed, what is the probability that a new oil filter is needed?
The probability that a car being filled with petrol will also need an oil change is 0.30; the probability that it needs a new oil filter is 0.40; and the probability that both the oil and filter need changing is 0.15. If a new oil filter is needed, what is the probability that the oil has to be changed?
One bag contains 5 white and 3 black balls. Another bag contains 4 white and 6 black balls. If one ball is drawn from each bag, find the probability that one white and one black
Two thirds of students in a class are boys and rest girls. It is known that the probability of a girl getting a first grade is 0.85 and that of boys is 0.70. Find the probability that a student chosen at random will get first grade marks.
Find the probability that in 10 throws of a fair die a score which is a multiple of 3 will be obtained in at least 8 of the throws.
If P(A ∩ B) = `7/10` and P(B) = `17/20`, then P(A|B) equals ______.
If P(A) = `3/10`, P(B) = `2/5` and P(A ∪ B) = `3/5`, then P(B|A) + P(A|B) equals ______.
Two cards are drawn out randomly from a pack of 52 cards one after the other, without replacement. The probability of first card being a king and second card not being a king is:
A pack of cards has one card missing. Two cards are drawn randomly and are found to be spades. The probability that the missing card is not a spade, is ______.
It is given that the events A and B are such that P(A) = `1/4, P(A/B) = 1/2` and `P(B/A) = 2/3`, then P(B) is equal to ______.
If the sum of numbers obtained on throwing a pair of dice is 9, then the probability that number obtained on one of the dice is 4, is ______.
