Advertisements
Advertisements
प्रश्न
In a college, 70% of students pass in Physics, 75% pass in Mathematics and 10% of students fail in both. One student is chosen at random. What is the probability that:
(i) He passes in Physics and Mathematics?
(ii) He passes in Mathematics given that he passes in Physics.
(iii) He passes in Physics given that he passes in Mathematics.
उत्तर
Let x% of students pass in both Physics and Mathematics
Students pass in Physics = 70% ⇒ P (P) = `(70)/(100)`
Students pass in Mathematics = 75% ⇒ P (M) = `(75)/(100)`
Students fail in both = 10%
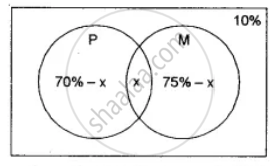
Now students pass in physics only + students pass in mathematics only + students pass in both physics and mathematics = 90%
⇒ 70% - x + x + 75% - x = 90%
x = 55% ⇒ P (M ∩ P) = `(55)/(100)`
(i)
P ( Passes in Physics and Mathematics) = `(55)/(100) = (11)/(20)`
(ii)
P (M/P) = `(P (M ∩ P))/(P(P)`
= `((55)/(100))/(70/(100))`
= `(55)/(70) = (11)/(14)`
(iii)
`P(P/M) = (P(M ∩ P))/(P(M))`
`(55/100)/(75/100)`
= `55/75 = 11/15`
APPEARS IN
संबंधित प्रश्न
40% students of a college reside in hostel and the remaining reside outside. At the end of the year, 50% of the hostelers got A grade while from outside students, only 30% got A grade in the examination. At the end of the year, a student of the college was chosen at random and was found to have gotten A grade. What is the probability that the selected student was a hosteler ?
If P(A) = 0.8, P(B) = 0.5 and P(B|A) = 0.4, find P(A ∪ B)
If `P(A) = 6/11, P(B) = 5/11 "and" P(A ∪ B) = 7/11` find
- P(A ∩ B)
- P(A|B)
- P(B|A)
Determine P(E|F).
A coin is tossed three times, where
E: at least two heads, F: at most two heads
Determine P(E|F).
Two coins are tossed once, where
E: tail appears on one coin, F: one coin shows head
A fair die is rolled. Consider events E = {1, 3, 5}, F = {2, 3} and G = {2, 3, 4, 5} Find P (E|G) and P (G|E)
Consider the experiment of throwing a die, if a multiple of 3 comes up, throw the die again and if any other number comes, toss a coin. Find the conditional probability of the event ‘the coin shows a tail’, given that ‘at least one die shows a 3’.
If events A and B are independent, such that `P(A)= 3/5`, `P(B)=2/3` 'find P(A ∪ B).
In an examination, 30% of students have failed in subject I, 20% of the students have failed in subject II and 10% have failed in both subject I and subject II. A student is selected at random, what is the probability that the student has failed in at least one subject?
A bag contains 10 white balls and 15 black balls. Two balls are drawn in succession without replacement. What is the probability that, one is white and other is black?
Two balls are drawn from an urn containing 5 green, 3 blue, and 7 yellow balls one by one without replacement. What is the probability that at least one ball is blue?
Select the correct option from the given alternatives :
Bag I contains 3 red and 4 black balls while another Bag II contains 5 red and 6 black balls. One ball is drawn at random from one of the bags and it is found to be red. The probability that it was drawn from Bag II
Can two events be mutually exclusive and independent simultaneously?
If for two events A and B, P(A) = `3/4`, P(B) = `2/5` and A ∪ B = S (sample space), find the conditional probability P(A/B)
The probability that a car being filled with petrol will also need an oil change is 0.30; the probability that it needs a new oil filter is 0.40; and the probability that both the oil and filter need changing is 0.15. If the oil had to be changed, what is the probability that a new oil filter is needed?
The probability that a car being filled with petrol will also need an oil change is 0.30; the probability that it needs a new oil filter is 0.40; and the probability that both the oil and filter need changing is 0.15. If a new oil filter is needed, what is the probability that the oil has to be changed?
Given P(A) = 0.4 and P(A ∪ B) = 0.7 Find P(B) if P(A/B) = 0.4
A year is selected at random. What is the probability that it contains 53 Sundays
In a multiple-choice question, there are three options out of which only one is correct. A person is guessing the answer at random. If there are 7 such questions, then the probability that he will get exactly 4 correct answers is ______
If X denotes the number of ones in five consecutive throws of a dice, then P(X = 4) is ______
Three machines E1, E2, E3 in a certain factory produced 50%, 25% and 25%, respectively, of the total daily output of electric tubes. It is known that 4% of the tubes produced one each of machines E1 and E2 are defective, and that 5% of those produced on E3 are defective. If one tube is picked up at random from a day’s production, calculate the probability that it is defective.
If P(A) = `3/10`, P(B) = `2/5` and P(A ∪ B) = `3/5`, then P(B|A) + P(A|B) equals ______.
If P(A) = 0.4, P(B) = 0.8 and P(B|A) = 0.6, then P(A ∪ B) is equal to ______.
If A and B are two events such that P(A) = `1/3`, P(B) = `1/5` and P(A ∪ B) = `1/2`, then P(A|B') + P(B|A') is equal to ______.
A Problem in Mathematics is given to the three students A, B and C. Their chances of solving the problem are `1/2, 1/3` and `1/4` respectively. Find the probability that exactly two students will solve the problem.
Students of under graduation submitted a case study on “Understanding the Probability of Left-Handedness in Children Based on Parental Handedness”. Following Recent studies suggest that roughly 12% of the world population is left-handed. Depending on the parents’ handedness, the chances of having a left-handed child are as follows:
Scenario A: Both parents are left-handed, with a 24% chance of the child being left-handed.
Scenario B: The fathers is right-handed and the mothers left-handed, with a 22% chance of child being left-handed.
Scenario C: The fathers left-handed and the mother is right-handed, with a 17% chance of child being left-handed.
Scenario D: Both parents are right-handed, with a 9% chance of having a left-handed child.
Assuming that scenarios A, B, C and D are equally likely and L denotes the event that the child is left-handed, answer the following questions.
- What is the overall probability that a randomly selected child is left-handed?
- Given that exactly one parent is left-handed, what is the probability that a randomly selected child is left-handed?
- If a child is left-handed, what is the probability that both parents are left-handed?
