Advertisements
Advertisements
प्रश्न
In a non-leap year, the probability of having 53 tuesdays or 53 wednesdays is ______.
विकल्प
`1/7`
`2/7`
`3/7`
None of these
उत्तर
In a non-leap year, the probability of having 53 tuesdays or 53 wednesdays is `1/7`.
Explanation:
There are 365 days in a non-leap year and there are 7 days in a week
∴ 365 ÷ 7 = 52 weeks + 1 day
So, this day may be Tuesday or Wednesday.
So, the required probability = `1/7`.
APPEARS IN
संबंधित प्रश्न
A card is selected from a pack of 52 cards.
- How many points are there in the sample space?
- Calculate the probability that the card is an ace of spades.
- Calculate the probability that the card is
- an ace
- black card.
In a lottery, person chooses six different natural numbers at random from 1 to 20, and if these six numbers match with the six numbers already fixed by the lottery committee, he wins the prize. What is the probability of winning the prize in the game? [Hint: order of the numbers is not important.]
Check whether the following probabilities P(A) and P(B) are consistently defined
P(A) = 0.5, P(B) = 0.7, P(A ∩ B) = 0.6
A box contains 10 red marbles, 20 blue marbles and 30 green marbles. 5 marbles are drawn from the box, what is the probability that all will be blue?
A and B throw a pair of dice. If A throws 9, find B's chance of throwing a higher number.
Two unbiased dice are thrown. Find the probability that the total of the numbers on the dice is greater than 10.
Two unbiased dice are thrown. Find the probability that the sum of the numbers obtained on the two dice is neither a multiple of 2 nor a multiple of 3
If a letter is chosen at random from the English alphabet, find the probability that the letter is a consonant .
Which of the cannot be valid assignment of probability for elementary events or outcomes of sample space S = {w1, w2, w3, w4, w5, w6, w7}:
| Elementary events: | w1 | w2 | w3 | w4 | w5 | w6 | w7 |
| (iii) | 0.7 | 0.06 | 0.05 | 0.04 | 0.03 | 0.2 | 0.1 |
Which of the cannot be valid assignment of probability for elementary events or outcomes of sample space S = {w1, w2, w3, w4, w5, w6, w7}:
| Elementary events: | w1 | w2 | w3 | w4 | w5 | w6 | w7 |
| (iv) |
\[\frac{1}{14}\]
|
\[\frac{2}{14}\]
|
\[\frac{3}{14}\]
|
\[\frac{4}{14}\]
|
\[\frac{5}{14}\]
|
\[\frac{6}{14}\]
|
\[\frac{15}{14}\]
|
Two dice are thrown together. The probability that neither they show equal digits nor the sum of their digits is 9 will be
An urn contains twenty white slips of paper numbered from 1 through 20, ten red slips of paper numbered from 1 through 10, forty yellow slips of paper numbered from 1 through 40, and ten blue slips of paper numbered from 1 through 10. If these 80 slips of paper are thoroughly shuffled so that each slip has the same probability of being drawn. Find the probabilities of drawing a slip of paper that is blue or white
An urn contains twenty white slips of paper numbered from 1 through 20, ten red slips of paper numbered from 1 through 10, forty yellow slips of paper numbered from 1 through 40, and ten blue slips of paper numbered from 1 through 10. If these 80 slips of paper are thoroughly shuffled so that each slip has the same probability of being drawn. Find the probabilities of drawing a slip of paper that is numbered 1, 2, 3, 4 or 5
An urn contains twenty white slips of paper numbered from 1 through 20, ten red slips of paper numbered from 1 through 10, forty yellow slips of paper numbered from 1 through 40, and ten blue slips of paper numbered from 1 through 10. If these 80 slips of paper are thoroughly shuffled so that each slip has the same probability of being drawn. Find the probabilities of drawing a slip of paper that is red or yellow and numbered 1, 2, 3 or 4
In a leap year the probability of having 53 Sundays or 53 Mondays is ______.
Four candidates A, B, C, D have applied for the assignment to coach a school cricket team. If A is twice as likely to be selected as B, and B and C are given about the same chance of being selected, while C is twice as likely to be selected as D, what are the probabilities that A will not be selected?
The accompanying Venn diagram shows three events, A, B, and C, and also the probabilities of the various intersections (for instance, P(A ∩ B) = .07). Determine P(A)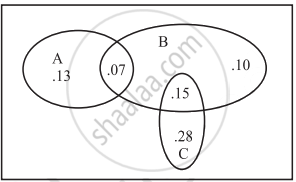
The accompanying Venn diagram shows three events, A, B, and C, and also the probabilities of the various intersections (for instance, P(A ∩ B) = .07). Determine `P(A ∩ barB)`
The accompanying Venn diagram shows three events, A, B, and C, and also the probabilities of the various intersections (for instance, P(A ∩ B) = .07). Determine Probability of exactly one of the three occurs
A bag contains 8 red and 5 white balls. Three balls are drawn at random. Find the probability that all the three balls are white
If the letters of the word ASSASSINATION are arranged at random. Find the probability that two I’s and two N’s come together
If the letters of the word ASSASSINATION are arranged at random. Find the probability that no two A’s are coming together
Three numbers are chosen from 1 to 20. Find the probability that they are not consecutive ______.
6 boys and 6 girls sit in a row at random. The probability that all the girls sit together is ______.
The probability that a person visiting a zoo will see the giraffee is 0.72, the probability that he will see the bears is 0.84 and the probability that he will see both is 0.52.
A box contains 10 red marbles, 20 blue marbles and 30 green marbles. 5 marbles are drawn from the box, what is the probability that atleast one will be green?
