Advertisements
Advertisements
प्रश्न
In following fig., chords PQ and RS of a circle intersect at T. If RS = 18cm, ST = 6cm and PT = 18cm, find the length of TQ.

उत्तर
Let TQ = x cm
In Δ PTR and Δ STQ
∠ TPR = ∠ TSQ (angles in the same segment)
∠ PTR = ∠ STQ (vertically opposite L's)
∴ ∠ PTR = ∠ STQ {AA corollary)
`"PT"/"ST" = "TR"/"TQ"` (similar sides of similar triangles)
`18/6 = 12/"x"`
= x = 4
⇒ TQ = 4 cm
APPEARS IN
संबंधित प्रश्न
AB and CD are two equal chords of a circle with centre O which intersect each other at right
angle at point P. If OM⊥ AB and ON ⊥ CD; show that OMPN is a square.
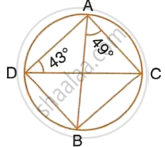
In the following figure, O is the centre of the circle. Find the values of a, b and c.

In the following figure, O is the centre of the circle. Find the values of a, b, c and d.
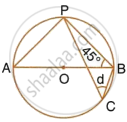
Calculate:
- ∠CDB,
- ∠ABC,
- ∠ACB.
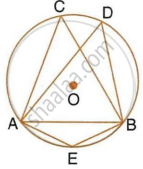
In the following figure, O is centre of the circle and ΔABC is equilateral.
Find:
- ∠ADB,
- ∠AEB.
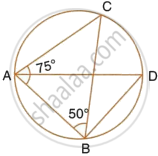
Given: ∠CAB = 75° and ∠CBA = 50°. Find the value of ∠DAB + ∠ABD.
The line joining the midpoints of two chords of a circle passes through its center.
Prove that the chords are parallel.
If two chords of a circle are equally inclined to the diameter through their point of intersection, prove that the chords are equal.
AB and CD are two chords of a circle such that AB = 6 cm, CD = 12 cm and AB || CD. If the distance between AB and CD is 3 cm, find the radius of the circle.
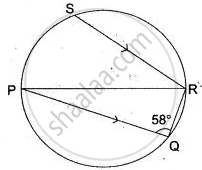
In the adjoining figure, PQ is the diameter, chord SR is parallel to PQ. Give ∠ PQR = 58°.
Calculate:
(i) ∠ RPQ,
(ii) ∠ STP ( T is a point on the minor arc)