Advertisements
Advertisements
प्रश्न
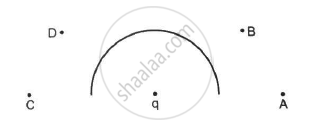
In the following figure shows a charge q placed at the centre of a hemisphere. A second charge Q is placed at one of the positions A, B, C and D. In which position(s) of this second charge, the flux of the electric field through the hemisphere remains unchanged?
(a) A
(b) B
(c) C
(d) D
उत्तर
(a) A
(c) C
These are the only points in the straight line with the charge q and at the brim of the hemisphere. So, field lines emerging from these charges do not affect the flux through the hemisphere due to charge q. On the other hand, the two remaining charges are beside the surface of the hemisphere and not in line with the charge q and not at the brim. So, they will affect the flux. Hence, the correct answers are (a) and (c).
APPEARS IN
संबंधित प्रश्न
Two identical circular loops 1 and 2 of radius R each have linear charge densities −λ and +λ C/m respectively. The loops are placed coaxially with their centres `Rsqrt3` distance apart. Find the magnitude and direction of the net electric field at the centre of loop 1.
Show that there can be no net charge in a region in which the electric field is uniform at all points.
The electric field in a region is given by
`vec"E"= 3/5"E"_0 vec"i" + 4/5 "E"_0 vec "i" "with" " E"_0 = 2.0 xx 10^3 "N""C"^-1.`
Find the flux of this field through a rectangular surface of area 0⋅2 m2 parallel to the y-z plane.
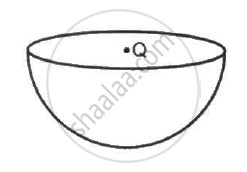
A charge Q is placed at the centre of an imaginary hemispherical surface. Using symmetry arguments and Gauss's Law, find the flux of the electric field due to this charge through the surface of the hemisphere in the following figure.
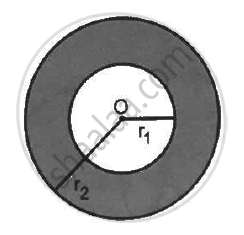
A charge Q is distributed uniformly within the material of a hollow sphere of inner and outer radii r1 and r2 (see the figure). Find the electric field at a point P at a distance x away from the centre for r1 < x < r. Draw a rough graph showing the electric field as a function of x for 0 < x < 2r2 (see the figure).
A charge Q is placed at the centre of an uncharged, hollow metallic sphere of radius a. (a) Find the surface. (b) If a charge q is put on the sphere, what would be the surface charge densities on the inner and outer surfaces? (c) Find the electric field inside the sphere at a distance x from the centre in the situations (a) and (b).
Consider the following very rough model of a beryllium atom. The nucleus has four protons and four neutrons confined to a small volume of radius 10−15 m. The two 1 selectrons make a spherical charge cloud at an average distance of 1⋅3 ×10−11 m from the nucleus, whereas the two 2 s electrons make another spherical cloud at an average distance of 5⋅2 × 10−11 m from the nucleus. Find three electric fields at (a) a point just inside the 1 s cloud and (b) a point just inside the 2 s cloud.
A charged particle with a charge of −2⋅0 × 10−6 C is placed close to a non-conducting plate with a surface charge density of 4.0 × 10-6Cm0-2. Find the force of attraction between the particle and the plate.
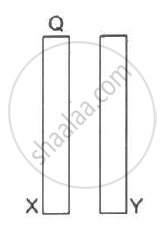
Two conducting plates X and Y, each with a large surface area A (on one side), are placed parallel to each other, as shown in the following figure . Plate X is given a charge Q,whereas the other is kept neutral. Find (a) the surface charge density at the inner surface of plate X (b) the electric field at a point to the left of the plates (c) the electric field at a point in between the plates and (d) the electric field at a point to the right of the plates.
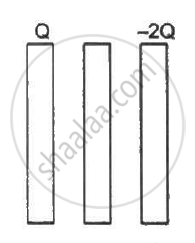
Three identical metal plates with large surface areas are kept parallel to each other as shown in the following figure. The leftmost plate is given a charge Q, the rightmost a charge −2Q and the middle one is kept neutral. Find the charge appearing on the outer surface of the rightmost plate.
A uniform electric field of 10 N C−1 exists in the vertically downward direction. Find the increase in the electric potential as one goes up through a height of 50 cm.
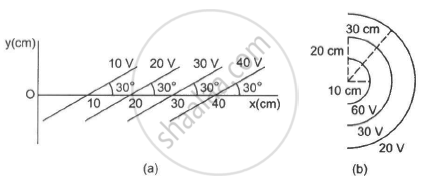
Some equipotential surface is shown in the figure. What can you say about the magnitude and the direction of the electric field?
A uniform field of 2.0 NC−1 exists in space in the x-direction. (a) Taking the potential at the origin to be zero, write an expression for the potential at a general point (x, y, z). (b) At which point, the potential is 25 V? (c) If the potential at the origin is taken to be 100 V, what will be the expression for the potential at a general point? (d) What will be the potential at the origin if the potential at infinity is taken to be zero? Is it practical to choose the potential at infinity to be zero?
When a comb rubbed with dry hair attracts pieces of paper. This is because the ______.
