Advertisements
Advertisements
प्रश्न
किसी कक्षा के विद्यार्थियों की एक मेडिकल परीक्षा में निम्नलिखित रक्त समूह रिकार्ड किए गए :
| रक्त समूह | A | AB | B | O |
| विद्यार्थियों का समूह | 10 | 13 | 12 | 5 |
इस कक्षा में से एक विद्यार्थी यादृच्छिक रूप से चुना जाता है। इस विद्यार्थी का रक्त समूह B होने की प्रायिकता है :
विकल्प
`1/4`
`13/40`
`3/10`
`1/8`
उत्तर
`bb(3/10)`
स्पष्टीकरण -
एक मेडिकल परीक्षा में कुल छात्रों की संख्या, n(S) = 40
B रक्त समूह वाले व्यक्तियों की संख्या, n(E) = 12
∴ संभावना है कि उसका रक्त समूह B है = `(n(E))/(n(S)) = 12/40 = 3/10`
अतः, संभावना है कि उसका रक्त समूह B है `3/10`
APPEARS IN
संबंधित प्रश्न
निम्न स्थिति पर आधारित एक उदाहरण दीजिए।
- माध्य की केंद्रीय प्रवृत्ति का उपयुक्त माप है।
- माध्य केंद्रीय प्रवृत्ति का उपयुक्त माप नहीं है, जबकि माध्यक एक उपयुक्त माप है।
यदि x1, x2, ..., xn का माध्य `barx` है, y1, y2, ..., yn का माध्य `bary` है तथा x1, x2, ..., xn, y1, y2, ..., yn का माध्य `barz` है, तो `barz` बराबर है :
यदि `barx_1, barx_2, barx_3, ..., barx_n` क्रमश : प्रेक्षणों की संख्या n1, n2, ..., nn वाले n समूहों के माध्य हैं, तो सभी समूहों को मिलाकर लेने पर उनका माध्य `barx` निम्नलिखित से प्राप्त होता है :
25 प्रेक्षणों का माध्य 36 है। इन प्रेक्षणों में से यदि प्रथम 13 प्रेक्षणों का माध्य 32 है तथा अंतिम 13 का माध्य 40 है तो 13वाँ प्रेक्षण है :
19 – 36 महीने की आयु वाले 364 बच्चों पर किए गए एक सर्वे में यह पाया गया कि 91 बच्चे आलू के चिप्स खाना पसंद करते हैं। इनमें से एक बच्चा यदि यादृच्छिक (यदृच्छ) रूप से चुना जाता है तो इसकी प्रायिकता कि वह बच्चा आलू के चिप्स पसंद नहीं करेगा, है :
एक संग्रह में से 80 बल्ब यादृच्छिक रूप से चुने जाते हैं और उनके जीवन कालों (घंटों में) को निम्नलिखित बारंबारता सारणी के रूप में रिकार्ड किया गया :
| जीवन काल (घंटों में) | 300 | 500 | 700 | 900 | 1100 |
| बारंबारता | 10 | 12 | 23 | 25 | 10 |
इस संग्रह में से एक बल्ब यादृच्छिक रूप से चुना जाता है। इस बल्ब का जीवन काल 1150 घंटा होने की प्रायिकता है :
50 प्रेक्षणों का माध्य 80.4 प्राप्त हुआ। परंतु बाद में यह ज्ञात हुआ कि एक स्थान पर 96 को 69 पढ़ लिया गया है। सही माध्य ज्ञात कीजिए।
निम्नलिखित आकृति में, एक आयतचित्र दिया है जो किसी फैक्ट्री की श्रमिकों की दैनिक मजदूरी दर्शाता है। इसके लिए एक बारंबारता बंटन सारणी की रचना कीजिए।
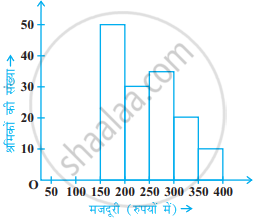
निम्नलिखित बंटन का माध्य 50 है।
| x | f |
| 10 | 17 |
| 30 | 5a + 3 |
| 50 | 32 |
| 70 | 7a – 11 |
| 90 | 19 |
a का मान ज्ञात कीजिए और फिर 30 और 70 की बारंबारता ज्ञात कीजिए।
किसी परीक्षा में लड़के और लड़कियों के (100 में से) प्राप्त अंकों के माध्य क्रमश : 70 और 73 हैं। यदि इसी परीक्षा में, सभी विद्यार्थियों के प्राप्तांकों का माध्य 71 है, तो लड़के और लड़कियों की संख्याओं का अनुपात ज्ञात कीजिए।
