Advertisements
Advertisements
प्रश्न
Let f: R → R be defined by f(x) = 3x – 4. Then f–1(x) is given by ______.
विकल्प
`(x + 4)/3`
`x/3 - 4`
3x + 4
None of these
उत्तर
Let f: R → R be defined by f(x) = 3x – 4. Then f–1(x) is given by `(x + 4)/3`.
APPEARS IN
संबंधित प्रश्न
Check the injectivity and surjectivity of the following function:
f: N → N given by f(x) = x2
Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from A to B. Show that f is one-one.
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = 3 − 4x
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = 1 + x2
Find gof and fog when f : R → R and g : R → R is defined by f(x) = 2x + 3 and g(x) = x2 + 5 .
Find gof and fog when f : R → R and g : R → R is defined by f(x) = 2x + x2 and g(x) = x3
Let f = {(3, 1), (9, 3), (12, 4)} and g = {(1, 3), (3, 3) (4, 9) (5, 9)}. Show that gof and fog are both defined. Also, find fog and gof.
Let f : R → R and g : R → R be defined by f(x) = x2 and g(x) = x + 1. Show that fog ≠ gof.
Consider f : N → N, g : N → N and h : N → R defined as f(x) = 2x, g(y) = 3y + 4 and h(z) = sin z for all x, y, z ∈ N. Show that ho (gof) = (hog) of.
Consider f : R → R given by f(x) = 4x + 3. Show that f is invertible. Find the inverse of f.
Let f : [−1, ∞) → [−1, ∞) be given by f(x) = (x + 1)2 − 1, x ≥ −1. Show that f is invertible. Also, find the set S = {x : f(x) = f−1 (x)}.
Let A and B be two sets, each with a finite number of elements. Assume that there is an injective map from A to B and that there is an injective map from B to A. Prove that there is a bijection from A to B.
Which of the following graphs represents a one-one function?
If f : {5, 6} → {2, 3} and g : {2, 3} → {5, 6} are given by f = {(5, 2), (6, 3)} and g = {(2, 5), (3, 6)}, then find fog. [NCERT EXEMPLAR]
The function \[f : R \to R\] defined by
\[f\left( x \right) = 6^x + 6^{|x|}\] is
Let
\[A = \left\{ x \in R : x \geq 1 \right\}\] The inverse of the function,
\[f : A \to A\] given by
\[f\left( x \right) = 2^{x \left( x - 1 \right)} , is\]
If A = {a, b, c, d} and f = {a, b), (b, d), (c, a), (d, c)}, show that f is one-one from A onto A. Find f–1
Are the following set of ordered pairs functions? If so, examine whether the mapping is injective or surjective.
{(a, b): a is a person, b is an ancestor of a}
The function f : R → R defined by f(x) = 3 – 4x is ____________.
An organization conducted a bike race under 2 different categories-boys and girls. Totally there were 250 participants. Among all of them finally, three from Category 1 and two from Category 2 were selected for the final race. Ravi forms two sets B and G with these participants for his college project. Let B = {b1,b2,b3} G={g1,g2} where B represents the set of boys selected and G the set of girls who were selected for the final race.
Ravi decides to explore these sets for various types of relations and functions.
- Ravi wants to know among those relations, how many functions can be formed from B to G?
Raji visited the Exhibition along with her family. The Exhibition had a huge swing, which attracted many children. Raji found that the swing traced the path of a Parabola as given by y = x2.
Answer the following questions using the above information.
- Let f: {1,2,3,....} → {1,4,9,....} be defined by f(x) = x2 is ____________.
A function f: x → y is/are called onto (or surjective) if x under f.
Let [x] denote the greatest integer ≤ x, where x ∈ R. If the domain of the real valued function f(x) = `sqrt((|[x]| - 2)/(|[x]| - 3)` is (–∞, a) ∪ [b, c) ∪ [4, ∞), a < b < c, then the value of a + b + c is ______.
If log102 = 0.3010.log103 = 0.4771 then the number of ciphers after decimal before a significant figure comes in `(5/3)^-100` is ______.
`x^(log_5x) > 5` implies ______.
If f: [0, 1]→[0, 1] is defined by f(x) = `(x + 1)/4` and `d/(dx) underbrace(((fofof......of)(x)))_("n" "times")""|_(x = 1/2) = 1/"m"^"n"`, m ∈ N, then the value of 'm' is ______.
Let f(x) = ax (a > 0) be written as f(x) = f1(x) + f2(x), where f1(x) is an even function and f2(x) is an odd function. Then f1(x + y) + f1(x – y) equals ______.
The graph of the function y = f(x) is symmetrical about the line x = 2, then ______.
Which one of the following graphs is a function of x?
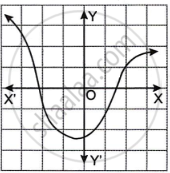 |
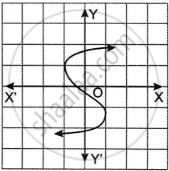 |
| Graph A | Graph B |
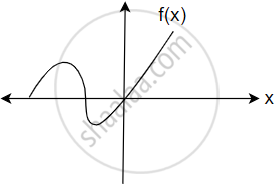
The given function f : R → R is not ‘onto’ function. Give reason.
