Advertisements
Advertisements
प्रश्न
Let f = {(3, 1), (9, 3), (12, 4)} and g = {(1, 3), (3, 3) (4, 9) (5, 9)}. Show that gof and fog are both defined. Also, find fog and gof.
उत्तर
f = {(3, 1), (9, 3), (12, 4)} and g = {(1, 3), (3, 3) (4, 9) (5, 9)}
f : {3, 9, 12} → {1, 3,4} and g : {1, 3, 4, 5} → {3, 9}
Co-domain of f is a subset of the domain of g.
So, gof exists and gof : {3, 9, 12} → {3, 9}
(gof) (3)=g (f (3))=g (1) =3
(gof) (9)=g (f (9))=g (3)=3
(gof) (12)=g (f (12))=g (4)=9
⇒ gof ={(3, 3), (9, 3), (12, 9)}
Co-domain of g is a subset of the domain of f.
So, fog exists and fog : {1, 3, 4, 5} → {3, 9, 12}
(fog) (1)=f (g (1))=f (3)=1
(fog) (3)=f (g (3))=f (3)=1
(fog) (4)=f (g (4))=f (9)=3
(fog) (5)=f (g (5))=f (9)=3
⇒ fog={(1, 1), (3, 1), (4, 3), (5, 3)}
APPEARS IN
संबंधित प्रश्न
Show that the function f in `A=R-{2/3} ` defined as `f(x)=(4x+3)/(6x-4)` is one-one and onto hence find f-1
Check the injectivity and surjectivity of the following function:
f: N → N given by f(x) = x3
Show that the modulus function f: R → R given by f(x) = |x| is neither one-one nor onto, where |x| is x, if x is positive or 0 and |x| is − x if x is negative.
Find the number of all onto functions from the set {1, 2, 3, …, n} to itself.
Which of the following functions from A to B are one-one and onto?
f2 = {(2, a), (3, b), (4, c)} ; A = {2, 3, 4}, B = {a, b, c}
Which of the following functions from A to B are one-one and onto ?
f3 = {(a, x), (b, x), (c, z), (d, z)} ; A = {a, b, c, d,}, B = {x, y, z}.
Classify the following function as injection, surjection or bijection :
f : Q → Q, defined by f(x) = x3 + 1
Let A = [-1, 1]. Then, discuss whether the following function from A to itself is one-one, onto or bijective : `f (x) = x/2`
Give examples of two one-one functions f1 and f2 from R to R, such that f1 + f2 : R → R. defined by (f1 + f2) (x) = f1 (x) + f2 (x) is not one-one.
Give examples of two surjective functions f1 and f2 from Z to Z such that f1 + f2 is not surjective.
Let f : N → N be defined by
`f(n) = { (n+ 1, if n is odd),( n-1 , if n is even):}`
Show that f is a bijection.
[CBSE 2012, NCERT]
Find gof and fog when f : R → R and g : R → R is defined by f(x) = x2 + 8 and g(x) = 3x3 + 1 .
If f(x) = sin x and g(x) = 2x be two real functions, then describe gof and fog. Are these equal functions?
Consider f : {1, 2, 3} → {a, b, c} and g : {a, b, c} → {apple, ball, cat} defined as f (1) = a, f (2) = b, f (3) = c, g (a) = apple, g (b) = ball and g (c) = cat. Show that f, g and gof are invertible. Find f−1, g−1 and gof−1and show that (gof)−1 = f −1o g−1
Consider f : R → R+ → [4, ∞) given by f(x) = x2 + 4. Show that f is invertible with inverse f−1 of f given by f−1 `(x)= sqrt (x-4)` where R+ is the set of all non-negative real numbers.
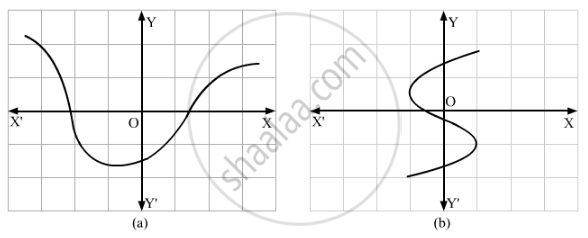
Which one of the following graphs represents a function?
If f : R → R is given by f(x) = x3, write f−1 (1).
Write whether f : R → R, given by `f(x) = x + sqrtx^2` is one-one, many-one, onto or into.
Let f : R → R be the function defined by f(x) = 4x − 3 for all x ∈ R Then write f . [NCERT EXEMPLAR]
If f(x) = 4 −( x - 7)3 then write f-1 (x).
Let\[A = \left\{ x \in R : - 1 \leq x \leq 1 \right\} = \text{B and C} = \left\{ x \in R : x \geq 0 \right\} and\]\[S = \left\{ \left( x, y \right) \in A \times B : x^2 + y^2 = 1 \right\} \text{and } S_0 = \left\{ \left( x, y \right) \in A \times C : x^2 + y^2 = 1 \right\}\]
Then,
A function f from the set of natural numbers to integers defined by
`{([n-1]/2," when n is odd" is ),(-n/2,when n is even ) :}`
Let
\[f : R - \left\{ n \right\} \to R\]
Mark the correct alternative in the following question:
Let f : R → R be given by f(x) = tanx. Then, f-1(1) is
Which function is used to check whether a character is alphanumeric or not?
Write about strlen() function.
Let f: R → R be the function defined by f(x) = 2x – 3 ∀ x ∈ R. write f–1
Are the following set of ordered pairs functions? If so, examine whether the mapping is injective or surjective.
{(x, y): x is a person, y is the mother of x}
Let f: R → R be defined by f(x) = `1/x` ∀ x ∈ R. Then f is ______.
Let f: `[2, oo)` → R be the function defined by f(x) = x2 – 4x + 5, then the range of f is ______.
The smallest integer function f(x) = [x] is ____________.
Let g(x) = x2 – 4x – 5, then ____________.
Range of `"f"("x") = sqrt((1 - "cos x") sqrt ((1 - "cos x")sqrt ((1 - "cos x")....infty))`
'If 'f' is a linear function satisfying f[x + f(x)] = x + f(x), then f(5) can be equal to:
Let f: R→R be a polynomial function satisfying f(x + y) = f(x) + f(y) + 3xy(x + y) –1 ∀ x, y ∈ R and f'(0) = 1, then `lim_(x→∞)(f(2x))/(f(x)` is equal to ______.
The graph of the function y = f(x) is symmetrical about the line x = 2, then ______.
Let f(x) be a polynomial function of degree 6 such that `d/dx (f(x))` = (x – 1)3 (x – 3)2, then
Assertion (A): f(x) has a minimum at x = 1.
Reason (R): When `d/dx (f(x)) < 0, ∀ x ∈ (a - h, a)` and `d/dx (f(x)) > 0, ∀ x ∈ (a, a + h)`; where 'h' is an infinitesimally small positive quantity, then f(x) has a minimum at x = a, provided f(x) is continuous at x = a.
Find the domain of sin–1 (x2 – 4).
Let A = R – {2} and B = R – {1}. If f: A `→` B is a function defined by f(x) = `(x - 1)/(x - 2)` then show that f is a one-one and an onto function.
