Advertisements
Advertisements
प्रश्न
Which of the following functions from A to B are one-one and onto ?
f3 = {(a, x), (b, x), (c, z), (d, z)} ; A = {a, b, c, d,}, B = {x, y, z}.
उत्तर
f3 = {(a, x), (b, x), (c, z), (d, z)} ; A = {a, b, c, d,}, B = {x, y, z}
Injectivity:
f3 (a) = x
f3 (b) = x
f3 (c) = z
f3 (d) = z
⇒ a and b have the same image x. (Also c and d have the same image z)
So, f3 is not one-one.
Surjectivity:
Co-domain of f1 ={x, y, z}
Range of f1 =set of images = {x, z}
So, the co-domain is not same as the range.
So, f3 is not onto.
APPEARS IN
संबंधित प्रश्न
Show that the function f: R* → R* defined by `f(x) = 1/x` is one-one and onto, where R* is the set of all non-zero real numbers. Is the result true if the domain R* is replaced by N, with co-domain being same as R?
Let A = R − {3} and B = R − {1}. Consider the function f: A → B defined by `f(x) = ((x- 2)/(x -3))`. Is f one-one and onto? Justify your answer.
Which of the following functions from A to B are one-one and onto?
f1 = {(1, 3), (2, 5), (3, 7)} ; A = {1, 2, 3}, B = {3, 5, 7}
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = x3 − x
Show that the function f : R − {3} → R − {2} given by f(x) = `(x-2)/(x-3)` is a bijection.
If A = {1, 2, 3}, show that a onto function f : A → A must be one-one.
Let f : N → N be defined by
`f(n) = { (n+ 1, if n is odd),( n-1 , if n is even):}`
Show that f is a bijection.
[CBSE 2012, NCERT]
Find gof and fog when f : R → R and g : R → R is defined by f(x) = 2x + x2 and g(x) = x3
Find gof and fog when f : R → R and g : R → R is defined by f(x) = x2 + 2x − 3 and g(x) = 3x − 4 .
Find fog and gof if : f (x) = x2 g(x) = cos x .
Let f be a real function given by f (x)=`sqrt (x-2)`
Find each of the following:
(i) fof
(ii) fofof
(iii) (fofof) (38)
(iv) f2
Also, show that fof ≠ `f^2` .
Consider f : R → R+ → [4, ∞) given by f(x) = x2 + 4. Show that f is invertible with inverse f−1 of f given by f−1 `(x)= sqrt (x-4)` where R+ is the set of all non-negative real numbers.
If f : R → (−1, 1) defined by `f (x) = (10^x- 10^-x)/(10^x + 10 ^-x)` is invertible, find f−1.
Let f : [−1, ∞) → [−1, ∞) be given by f(x) = (x + 1)2 − 1, x ≥ −1. Show that f is invertible. Also, find the set S = {x : f(x) = f−1 (x)}.
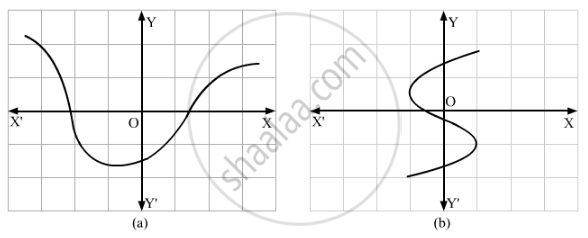
Which one of the following graphs represents a function?
Let \[f : \left( - \frac{\pi}{2}, \frac{\pi}{2} \right) \to R\] be a function defined by f(x) = cos [x]. Write range (f).
If f : R → R defined by f(x) = 3x − 4 is invertible, then write f−1 (x).
Let A = {x ∈ R : −4 ≤ x ≤ 4 and x ≠ 0} and f : A → R be defined by \[f\left( x \right) = \frac{\left| x \right|}{x}\]Write the range of f.
Let f : R → R+ be defined by f(x) = ax, a > 0 and a ≠ 1. Write f−1 (x).
Let f be an invertible real function. Write ( f-1 of ) (1) + ( f-1 of ) (2) +..... +( f-1 of ) (100 )
Write the domain of the real function f defined by f(x) = `sqrt (25 -x^2)` [NCERT EXEMPLAR]
Let
If \[f : R \to R is given by f\left( x \right) = 3x - 5, then f^{- 1} \left( x \right)\]
The inverse of the function
\[f : R \to \left\{ x \in R : x < 1 \right\}\] given by
\[f\left( x \right) = \frac{e^x - e^{- x}}{e^x + e^{- x}}\] is
Mark the correct alternative in the following question:
If the set A contains 7 elements and the set B contains 10 elements, then the number one-one functions from A to B is
Consider the set A containing n elements. Then, the total number of injective functions from A onto itself is ______
Let A = R – {3}, B = R – {1}. Let f: A → B be defined by f(x) = `(x - 2)/(x - 3)` ∀ x ∈ A . Then show that f is bijective
The function f : R → R defined by f(x) = 3 – 4x is ____________.
Let f : R → R be defind by f(x) = `1/"x" AA "x" in "R".` Then f is ____________.
Let f : [0, ∞) → [0, 2] be defined by `"f" ("x") = (2"x")/(1 + "x"),` then f is ____________.
If N be the set of all-natural numbers, consider f: N → N such that f(x) = 2x, ∀ x ∈ N, then f is ____________.
Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from A to B. Based on the given information, f is best defined as:
A function f: x → y is said to be one – one (or injective) if:
Prove that the function f is surjective, where f: N → N such that `f(n) = {{:((n + 1)/2",", if "n is odd"),(n/2",", if "n is even"):}` Is the function injective? Justify your answer.
If log102 = 0.3010.log103 = 0.4771 then the number of ciphers after decimal before a significant figure comes in `(5/3)^-100` is ______.
`x^(log_5x) > 5` implies ______.
The graph of the function y = f(x) is symmetrical about the line x = 2, then ______.
A function f : [– 4, 4] `rightarrow` [0, 4] is given by f(x) = `sqrt(16 - x^2)`. Show that f is an onto function but not a one-one function. Further, find all possible values of 'a' for which f(a) = `sqrt(7)`.
