Advertisements
Advertisements
प्रश्न
Let f be a real function given by f (x)=`sqrt (x-2)`
Find each of the following:
(i) fof
(ii) fofof
(iii) (fofof) (38)
(iv) f2
Also, show that fof ≠ `f^2` .
उत्तर
f (x) = `sqrt(x-2)`
For domain,
x − 2 ≥ 0
⇒ x ≥ 2
Domain of f = [ 2,∞ )
Since f is a square-root function, range of f =( 0,∞)
So, f : [2,∞) → ( 0,∞ )
(i) fof
Range of f is not a subset of the domain of f.
⇒Domain(fof)= { x : x ∈ domain of fand f (x) ∈ domain of f}
⇒ Domain (fof) = `{x :x in [2, ∞ ) and sqrt (x-2) in [ 2 ∞ )}`
⇒ Domain (fof) = `{x :x in [2, ∞ ) and sqrt (x-2)≥ 2 }`
⇒ Domain(fof) = { x : x ∈ [2,∞) and x−2 ≥4 }
⇒ Domain(fof) = { x : x ∈ [2,∞) and x ≥ 6}⇒ Domain(fof) = { x : x ≥ 6}
⇒ Domain(fof) = [ 6, ∞ )
fof : [6, ∞) → R
(fof) (x) = f (f (x))
= ` f (sqrt(x -2))`
= `sqrt (sqrt(x - 2) - 2)`
(ii) fofof= (fof) of
We have, f : [ 2,∞ ) → ( 0,∞ ) and fof : [ 6, ∞ ) → R
⇒ Range of f is not a subset of the domain of fof.
Then, domain((fof)of)={ x : x ∈domain of fand f (x) ∈ domain of fof }
⇒ Domain((fof)of) = `{ x : x in [ 2,∞) and sqrt (x-2) in [ 6 ,∞)}`
⇒ Domain ((fof)of) = ` x:x in [ 2 ∞ ) and sqrt(x-2) ≥ 6 }`
⇒ Domain ((fof)of) = { x : x ∈ [2,∞) and x − 2 ≥ 36}
⇒ Domain ((fof)of) = { x : x ∈ [2,∞) and x ≥ 38 }
⇒ Domain ((fof)of) = { x : x ≥ 38}
⇒ Domain ((fof)of) = [ 38, ∞ )
fof : [38,∞)→ R
So, ((fof)of) (x) = (fof) (f (x))
= (fof) `(sqrt(x-2))`
= `sqrt (sqrt (sqrt(x-2) -2 )-2)`
(iii) We have, (fofof) (x) = `sqrt (sqrt (sqrt(x-2) -2 )-2)`
So, (fofof) (38) = `sqrt (sqrt (sqrt(38-2) -2 )-2)`
=`sqrt (sqrt (sqrt(36) -2 )-2)`
=`sqrt (sqrt(6-2) -2 )`
= `sqrt (2 -2)`
= 0
(iv) We have, fof = `sqrt (sqrt(x-2) -2 )`
` f^2 (x) = f (x) xx f (x) = sqrt(x - 2) xx sqrt(x - 2) = x -2`
So, fof ≠ `f^2`
APPEARS IN
संबंधित प्रश्न
Let f: N → N be defined by f(n) = `{((n+1)/2, ",if n is odd"),(n/2,",n is even"):}` for all n ∈ N.
State whether the function f is bijective. Justify your answer.
Let f: R → R be defined as f(x) = 10x + 7. Find the function g: R → R such that g o f = f o g = 1R.
Show that function f: R `rightarrow` {x ∈ R : −1 < x < 1} defined by f(x) = `x/(1 + |x|)`, x ∈ R is one-one and onto function.
Given examples of two functions f: N → N and g: N → N such that gof is onto but f is not onto.
(Hint: Consider f(x) = x + 1 and `g(x) = {(x-1, ifx >1),(1, if x = 1):}`
Show that the function f: ℝ → ℝ defined by f(x) = `x/(x^2 + 1), ∀x in R`is neither one-one nor onto. Also, if g: ℝ → ℝ is defined as g(x) = 2x - 1. Find fog(x)
Classify the following function as injection, surjection or bijection : f : Z → Z given by f(x) = x2
Let A = {1, 2, 3}. Write all one-one from A to itself.
Show that the logarithmic function f : R0+ → R given by f (x) loga x ,a> 0 is a bijection.
Give examples of two one-one functions f1 and f2 from R to R, such that f1 + f2 : R → R. defined by (f1 + f2) (x) = f1 (x) + f2 (x) is not one-one.
Given A = {2, 3, 4}, B = {2, 5, 6, 7}. Construct an example of each of the following:
(i) an injective map from A to B
(ii) a mapping from A to B which is not injective
(iii) a mapping from A to B.
If f(x) = 2x + 5 and g(x) = x2 + 1 be two real functions, then describe each of the following functions:
(1) fog
(2) gof
(3) fof
(4) f2
Also, show that fof ≠ f2
Let f, g, h be real functions given by f(x) = sin x, g (x) = 2x and h (x) = cos x. Prove that fog = go (fh).
if f (x) = `sqrt (x +3) and g (x) = x ^2 + 1` be two real functions, then find fog and gof.
Let A and B be two sets, each with a finite number of elements. Assume that there is an injective map from A to B and that there is an injective map from B to A. Prove that there is a bijection from A to B.
Which of the following graphs represents a one-one function?
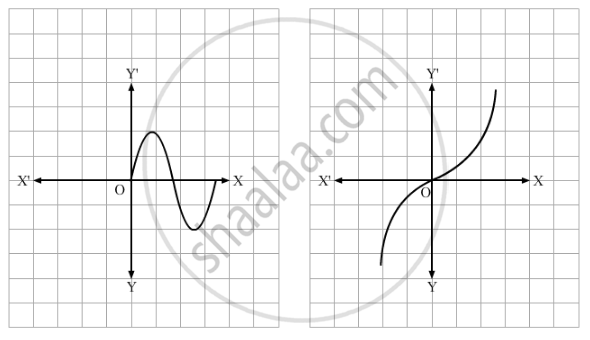
If A = {1, 2, 3} and B = {a, b}, write the total number of functions from A to B.
If f : R → R is defined by f(x) = x2, write f−1 (25)
If f : C → C is defined by f(x) = x2, write f−1 (−4). Here, C denotes the set of all complex numbers.
Let f be an invertible real function. Write ( f-1 of ) (1) + ( f-1 of ) (2) +..... +( f-1 of ) (100 )
Write the domain of the real function
`f (x) = sqrtx - [x] .`
Write the domain of the real function
`f (x) = 1/(sqrt([x] - x)`.
Which one the following relations on A = {1, 2, 3} is a function?
f = {(1, 3), (2, 3), (3, 2)}, g = {(1, 2), (1, 3), (3, 1)} [NCERT EXEMPLAR]
Write the domain of the real function f defined by f(x) = `sqrt (25 -x^2)` [NCERT EXEMPLAR]
If f(x) = 4 −( x - 7)3 then write f-1 (x).
The function
Let \[f\left( x \right) = \frac{1}{1 - x} . \text{Then}, \left\{ f o \left( fof \right) \right\} \left( x \right)\]
If \[g\left( x \right) = x^2 + x - 2\text{ and} \frac{1}{2} gof\left( x \right) = 2 x^2 - 5x + 2\] is equal to
If \[f : R \to R\] is given by \[f\left( x \right) = x^3 + 3, \text{then} f^{- 1} \left( x \right)\] is equal to
Mark the correct alternative in the following question:
Let f : R→ R be defined as, f(x) = \[\begin{cases}2x, if x > 3 \\ x^2 , if 1 < x \leq 3 \\ 3x, if x \leq 1\end{cases}\]
Then, find f( \[-\]1) + f(2) + f(4)
A function f: R→ R defined by f(x) = `(3x) /5 + 2`, x ∈ R. Show that f is one-one and onto. Hence find f−1.
Let f: R → R be defined by f(x) = `1/x` ∀ x ∈ R. Then f is ______.
Let f: `[2, oo)` → R be the function defined by f(x) = x2 – 4x + 5, then the range of f is ______.
The number of bijective functions from set A to itself when A contains 106 elements is ____________.
Let X = {-1, 0, 1}, Y = {0, 2} and a function f : X → Y defiend by y = 2x4, is ____________.
Raji visited the Exhibition along with her family. The Exhibition had a huge swing, which attracted many children. Raji found that the swing traced the path of a Parabola as given by y = x2.
Answer the following questions using the above information.
- Let f: N → N be defined by f(x) = x2 is ____________.
The domain of the function `cos^-1((2sin^-1(1/(4x^2-1)))/π)` is ______.
Let f(x) = ax (a > 0) be written as f(x) = f1(x) + f2(x), where f1(x) is an even function and f2(x) is an odd function. Then f1(x + y) + f1(x – y) equals ______.
