Advertisements
Advertisements
प्रश्न
If f : R → R is defined by f(x) = x2, write f−1 (25)
उत्तर
Let f−1 (25) =x ... (1)
⇒ f (x) = 25
⇒ x2 = 25
⇒ x2 − 25 = 0
⇒ (x−5) (x+5) = 0
⇒ x = ±5
⇒ f−1 (25) = {−5, 5} [from (1)]
APPEARS IN
संबंधित प्रश्न
Let f: N → N be defined by f(n) = `{((n+1)/2, ",if n is odd"),(n/2,",n is even"):}` for all n ∈ N.
State whether the function f is bijective. Justify your answer.
Give examples of two functions f: N → Z and g: Z → Z such that g o f is injective but gis not injective.
(Hint: Consider f(x) = x and g(x) =|x|)
If the function `f(x) = sqrt(2x - 3)` is invertible then find its inverse. Hence prove that `(fof^(-1))(x) = x`
Which of the following functions from A to B are one-one and onto?
f2 = {(2, a), (3, b), (4, c)} ; A = {2, 3, 4}, B = {a, b, c}
Classify the following function as injection, surjection or bijection : f : N → N given by f(x) = x3
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = sin2x + cos2x
Suppose f1 and f2 are non-zero one-one functions from R to R. Is `f_1 / f^2` necessarily one - one? Justify your answer. Here,`f_1/f_2 : R → R is given by (f_1/f_2) (x) = (f_1(x))/(f_2 (x)) for all x in R .`
Find gof and fog when f : R → R and g : R → R is defined by f(x) = 2x + 3 and g(x) = x2 + 5 .
Find gof and fog when f : R → R and g : R → R is defined by f(x) = x and g(x) = |x| .
Find gof and fog when f : R → R and g : R → R is defined by f(x) = 8x3 and g(x) = x1/3.
Let f : R → R and g : R → R be defined by f(x) = x2 and g(x) = x + 1. Show that fog ≠ gof.
Give examples of two functions f : N → Z and g : Z → Z, such that gof is injective but gis not injective.
Let f(x) = x2 + x + 1 and g(x) = sin x. Show that fog ≠ gof.
If f(x) = sin x and g(x) = 2x be two real functions, then describe gof and fog. Are these equal functions?
Let f be a real function given by f (x)=`sqrt (x-2)`
Find each of the following:
(i) fof
(ii) fofof
(iii) (fofof) (38)
(iv) f2
Also, show that fof ≠ `f^2` .
Let A = {1, 2, 3, 4}; B = {3, 5, 7, 9}; C = {7, 23, 47, 79} and f : A → B, g : B → C be defined as f(x) = 2x + 1 and g(x) = x2 − 2. Express (gof)−1 and f−1 og−1 as the sets of ordered pairs and verify that (gof)−1 = f−1 og−1.
If f : Q → Q, g : Q → Q are two functions defined by f(x) = 2 x and g(x) = x + 2, show that f and g are bijective maps. Verify that (gof)−1 = f−1 og −1.
If A = {1, 2, 3} and B = {a, b}, write the total number of functions from A to B.
If f : R → R defined by f(x) = 3x − 4 is invertible, then write f−1 (x).
Write the domain of the real function
`f (x) = 1/(sqrt([x] - x)`.
Write whether f : R → R, given by `f(x) = x + sqrtx^2` is one-one, many-one, onto or into.
If f(x) = x + 7 and g(x) = x − 7, x ∈ R, write fog (7).
\[f : R \to R \text{given by} f\left( x \right) = x + \sqrt{x^2} \text{ is }\]
The function f : R → R defined by
`f (x) = 2^x + 2^(|x|)` is
If \[g \left( f \left( x \right) \right) = \left| \sin x \right| \text{and} f \left( g \left( x \right) \right) = \left( \sin \sqrt{x} \right)^2 , \text{then}\]
If \[f\left( x \right) = \sin^2 x\] and the composite function \[g\left( f\left( x \right) \right) = \left| \sin x \right|\] then g(x) is equal to
Mark the correct alternative in the following question:
If the set A contains 7 elements and the set B contains 10 elements, then the number one-one functions from A to B is
A function f: R→ R defined by f(x) = `(3x) /5 + 2`, x ∈ R. Show that f is one-one and onto. Hence find f−1.
The function f : A → B defined by f(x) = 4x + 7, x ∈ R is ____________.
Which of the following functions from Z into Z is bijective?
An organization conducted a bike race under 2 different categories-boys and girls. Totally there were 250 participants. Among all of them finally, three from Category 1 and two from Category 2 were selected for the final race. Ravi forms two sets B and G with these participants for his college project. Let B = {b1,b2,b3} G={g1,g2} where B represents the set of boys selected and G the set of girls who were selected for the final race.
Ravi decides to explore these sets for various types of relations and functions.
- Let R: B → G be defined by R = { (b1,g1), (b2,g2),(b3,g1)}, then R is ____________.
Raji visited the Exhibition along with her family. The Exhibition had a huge swing, which attracted many children. Raji found that the swing traced the path of a Parabola as given by y = x2.
Answer the following questions using the above information.
- The function f: Z → Z defined by f(x) = x2 is ____________.
Let f: R→R be a continuous function such that f(x) + f(x + 1) = 2, for all x ∈ R. If I1 = `int_0^8f(x)dx` and I2 = `int_(-1)^3f(x)dx`, then the value of I1 + 2I2 is equal to ______.
Let f(1, 3) `rightarrow` R be a function defined by f(x) = `(x[x])/(1 + x^2)`, where [x] denotes the greatest integer ≤ x, Then the range of f is ______.
Let f(n) = `[1/3 + (3n)/100]n`, where [n] denotes the greatest integer less than or equal to n. Then `sum_(n = 1)^56f(n)` is equal to ______.
A function f : [– 4, 4] `rightarrow` [0, 4] is given by f(x) = `sqrt(16 - x^2)`. Show that f is an onto function but not a one-one function. Further, find all possible values of 'a' for which f(a) = `sqrt(7)`.
The function f(x) = [x], where [x] denotes the greatest integer less than or equal to x; is continuous at ______.
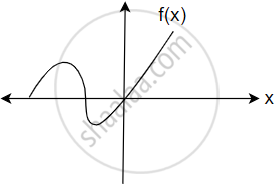
The given function f : R → R is not ‘onto’ function. Give reason.
