Advertisements
Advertisements
प्रश्न
If f : R → R is defined by f(x) = x2, write f−1 (25)
उत्तर
Let f−1 (25) =x ... (1)
⇒ f (x) = 25
⇒ x2 = 25
⇒ x2 − 25 = 0
⇒ (x−5) (x+5) = 0
⇒ x = ±5
⇒ f−1 (25) = {−5, 5} [from (1)]
APPEARS IN
संबंधित प्रश्न
Let S = {a, b, c} and T = {1, 2, 3}. Find F−1 of the following functions F from S to T, if it exists.
F = {(a, 2), (b, 1), (c, 1)}
Give an example of a function which is one-one but not onto ?
Classify the following function as injection, surjection or bijection : f : N → N given by f(x) = x2
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = 5x3 + 4
If f : A → B is an injection, such that range of f = {a}, determine the number of elements in A.
Let A = [-1, 1]. Then, discuss whether the following function from A to itself is one-one, onto or bijective : g(x) = |x|
Find the number of all onto functions from the set A = {1, 2, 3, ..., n} to itself.
Find gof and fog when f : R → R and g : R → R is defined by f(x) = x and g(x) = |x| .
Let f = {(3, 1), (9, 3), (12, 4)} and g = {(1, 3), (3, 3) (4, 9) (5, 9)}. Show that gof and fog are both defined. Also, find fog and gof.
Let A = {a, b, c}, B = {u v, w} and let f and g be two functions from A to B and from B to A, respectively, defined as :
f = {(a, v), (b, u), (c, w)}, g = {(u, b), (v, a), (w, c)}.
Show that f and g both are bijections and find fog and gof.
If f : A → B and g : B → C are onto functions, show that gof is a onto function.
Find fog and gof if : f (x) = x+1, g (x) = sin x .
Find fog and gof if : f(x) = `x^2` + 2 , g (x) = 1 − `1/ (1-x)`.
Let f, g, h be real functions given by f(x) = sin x, g (x) = 2x and h (x) = cos x. Prove that fog = go (fh).
if f (x) = `sqrt (x +3) and g (x) = x ^2 + 1` be two real functions, then find fog and gof.
Show that the function f : Q → Q, defined by f(x) = 3x + 5, is invertible. Also, find f−1
Consider f : R+ → [−5, ∞) given by f(x) = 9x2 + 6x − 5. Show that f is invertible with `f^-1 (x) = (sqrt (x +6)-1)/3 .`
If A = {1, 2, 3} and B = {a, b}, write the total number of functions from A to B.
Let C denote the set of all complex numbers. A function f : C → C is defined by f(x) = x3. Write f−1(1).
Let f be an invertible real function. Write ( f-1 of ) (1) + ( f-1 of ) (2) +..... +( f-1 of ) (100 )
Let A = {1, 2, 3, 4} and B = {a, b} be two sets. Write the total number of onto functions from A to B.
If the mapping f : {1, 3, 4} → {1, 2, 5} and g : {1, 2, 5} → {1, 3}, given by f = {(1, 2), (3, 5), (4, 1)} and g = {(2, 3), (5, 1), (1, 3)}, then write fog. [NCERT EXEMPLAR]
Let\[A = \left\{ x \in R : - 1 \leq x \leq 1 \right\} = \text{B and C} = \left\{ x \in R : x \geq 0 \right\} and\]\[S = \left\{ \left( x, y \right) \in A \times B : x^2 + y^2 = 1 \right\} \text{and } S_0 = \left\{ \left( x, y \right) \in A \times C : x^2 + y^2 = 1 \right\}\]
Then,
If a function\[f : [2, \infty )\text{ to B defined by f}\left( x \right) = x^2 - 4x + 5\] is a bijection, then B =
Which of the following functions from
\[A = \left\{ x \in R : - 1 \leq x \leq 1 \right\}\]
If \[F : [1, \infty ) \to [2, \infty )\] is given by
\[f\left( x \right) = x + \frac{1}{x}, then f^{- 1} \left( x \right)\]
A function f: R→ R defined by f(x) = `(3x) /5 + 2`, x ∈ R. Show that f is one-one and onto. Hence find f−1.
Set A has 3 elements and the set B has 4 elements. Then the number of injective mappings that can be defined from A to B is ______.
Let X = {1, 2, 3}and Y = {4, 5}. Find whether the following subset of X ×Y are function from X to Y or not
h = {(1,4), (2, 5), (3, 5)}
Let X = {1, 2, 3}and Y = {4, 5}. Find whether the following subset of X ×Y are function from X to Y or not
k = {(1,4), (2, 5)}
Let A = {0, 1} and N be the set of natural numbers. Then the mapping f: N → A defined by f(2n – 1) = 0, f(2n) = 1, ∀ n ∈ N, is onto.
The function f : R → R defined by f(x) = 3 – 4x is ____________.
Let X = {-1, 0, 1}, Y = {0, 2} and a function f : X → Y defiend by y = 2x4, is ____________.
The function f: R → R defined as f(x) = x3 is:
Let R be a relation on the set L of lines defined by l1 R l2 if l1 is perpendicular to l2, then relation R is ____________.
`x^(log_5x) > 5` implies ______.
Let A = R – {2} and B = R – {1}. If f: A `→` B is a function defined by f(x) = `(x - 1)/(x - 2)` then show that f is a one-one and an onto function.
The trigonometric equation tan–1x = 3tan–1 a has solution for ______.
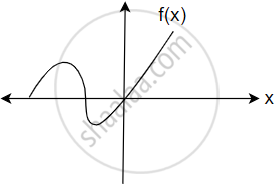
The given function f : R → R is not ‘onto’ function. Give reason.
