Advertisements
Advertisements
प्रश्न
Let A = R – {2} and B = R – {1}. If f: A `→` B is a function defined by f(x) = `(x - 1)/(x - 2)` then show that f is a one-one and an onto function.
उत्तर
Let A = R – {2}, B = R – {1}
f: A `→` B s.t. f(x) = `(x - 1)/(x - 2)`
For x1, x2 ∈ A
f(x1) = f(x2)
`\implies (x_1 - 1)/(x_1 - 2) = (x_2 - 1)/(x_2 - 2)`
`\implies (x_1 - 1)/(x_1 - 2) - 1 = (x_2 - 1)/(x_2 - 2) - 1`
`\implies 1/(x_1 - 2) = 1/(x_2 - 2)`
`\implies` x1 – 2 = x2 – 2
`\implies` x1 = x2
∴ f(x) is one-one function.
Also if f(x) = y, where y ∈ B.
`\implies (x - 1)/(x - 2)` = y
`\implies` x – 1 = xy – 2y
`\implies` 2y – 1 = xy – x
`\implies` 2y – 1 = x(y – 1)
x = `(2y - 1)/(y - 1) ∈ A`
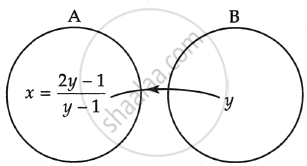
Clearly every element y ∈ B is associated to x = `(2y - 1)/(y - 1)` of set A.
So Range of f = B `\implies` f is into
Hence f is one-one and onto function.
APPEARS IN
संबंधित प्रश्न
Check the injectivity and surjectivity of the following function:
f: R → R given by f(x) = x2
Check the injectivity and surjectivity of the following function:
f: N → N given by f(x) = x3
Prove that the greatest integer function f: R → R, given by f(x) = [x], is neither one-one nor onto, where [x] denotes the greatest integer less than or equal to x.
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = sinx
Set of ordered pair of a function? If so, examine whether the mapping is injective or surjective :{(x, y) : x is a person, y is the mother of x}
Suppose f1 and f2 are non-zero one-one functions from R to R. Is `f_1 / f^2` necessarily one - one? Justify your answer. Here,`f_1/f_2 : R → R is given by (f_1/f_2) (x) = (f_1(x))/(f_2 (x)) for all x in R .`
Let f : R → R and g : R → R be defined by f(x) = x + 1 and g (x) = x − 1. Show that fog = gof = IR.
Consider f : N → N, g : N → N and h : N → R defined as f(x) = 2x, g(y) = 3y + 4 and h(z) = sin z for all x, y, z ∈ N. Show that ho (gof) = (hog) of.
If f : A → B and g : B → C are one-one functions, show that gof is a one-one function.
Find fog and gof if : f (x) = ex g(x) = loge x .
Find fog and gof if : f(x) = c, c ∈ R, g(x) = sin `x^2`
Let f be any real function and let g be a function given by g(x) = 2x. Prove that gof = f + f.
Let f be a real function given by f (x)=`sqrt (x-2)`
Find each of the following:
(i) fof
(ii) fofof
(iii) (fofof) (38)
(iv) f2
Also, show that fof ≠ `f^2` .
Show that the function f : Q → Q, defined by f(x) = 3x + 5, is invertible. Also, find f−1
If f : C → C is defined by f(x) = (x − 2)3, write f−1 (−1).
Write the domain of the real function
`f (x) = sqrtx - [x] .`
If a function g = {(1, 1), (2, 3), (3, 5), (4, 7)} is described by g(x) = \[\alpha x + \beta\] then find the values of \[\alpha\] and \[ \beta\] . [NCERT EXEMPLAR]
Let M be the set of all 2 × 2 matrices with entries from the set R of real numbers. Then, the function f : M→ R defined by f(A) = |A| for every A ∈ M, is
The function \[f : R \to R\] defined by
\[f\left( x \right) = 6^x + 6^{|x|}\] is
The inverse of the function
\[f : R \to \left\{ x \in R : x < 1 \right\}\] given by
\[f\left( x \right) = \frac{e^x - e^{- x}}{e^x + e^{- x}}\] is
If \[F : [1, \infty ) \to [2, \infty )\] is given by
\[f\left( x \right) = x + \frac{1}{x}, then f^{- 1} \left( x \right)\]
Mark the correct alternative in the following question:
Let A = {1, 2, ... , n} and B = {a, b}. Then the number of subjections from A into B is
If f(x) = `(x+3)/(4x−5) , "g"(x) = (3+5x)/(4x−1)` then verify that `("fog") (x)` = x.
For sets A, B and C, let f: A → B, g: B → C be functions such that g o f is injective. Then both f and g are injective functions.
Which of the following functions from Z into Z is bijective?
Let A = R – {3}, B = R – {1}. Let f : A → B be defined by `"f"("x") = ("x" - 2)/("x" - 3)` Then, ____________.
Let f: R → R defined by f(x) = 3x. Choose the correct answer
If A = {x ∈ R: |x – 2| > 1}, B = `{x ∈ R : sqrt(x^2 - 3) > 1}`, C = {x ∈ R : |x – 4| ≥ 2} and Z is the set of all integers, then the number of subsets of the set (A ∩ B ∩ C) C ∩ Z is ______.
Let f(x) be a polynomial of degree 3 such that f(k) = `-2/k` for k = 2, 3, 4, 5. Then the value of 52 – 10f(10) is equal to ______.
