Advertisements
Advertisements
प्रश्न
Write the domain of the real function
`f (x) = sqrtx - [x] .`
उत्तर
[x] is the greatest integral function.
\[So, 0\leq x - \left[ x \right] < 1\]
\[ \Rightarrow \sqrt{x - \left[ x \right] } \text{ exists for everyx} \in R . \]
\[\ \text{Rightarrow Domain }=R\]
APPEARS IN
संबंधित प्रश्न
Show that the function f: R* → R* defined by `f(x) = 1/x` is one-one and onto, where R* is the set of all non-zero real numbers. Is the result true if the domain R* is replaced by N, with co-domain being same as R?
Check the injectivity and surjectivity of the following function:
f: N → N given by f(x) = x2
Check the injectivity and surjectivity of the following function:
f: R → R given by f(x) = x2
Show that the modulus function f: R → R given by f(x) = |x| is neither one-one nor onto, where |x| is x, if x is positive or 0 and |x| is − x if x is negative.
Let f: R → R be the Signum Function defined as
f(x) = `{(1,x>0), (0, x =0),(-1, x< 0):}`
and g: R → R be the Greatest Integer Function given by g(x) = [x], where [x] is greatest integer less than or equal to x. Then does fog and gof coincide in (0, 1]?
Classify the following function as injection, surjection or bijection : f : N → N given by f(x) = x3
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = x3 − x
Find gof and fog when f : R → R and g : R → R is defined by f(x) = x2 + 2x − 3 and g(x) = 3x − 4 .
Let f(x) = x2 + x + 1 and g(x) = sin x. Show that fog ≠ gof.
Let A = {1, 2, 3, 4}; B = {3, 5, 7, 9}; C = {7, 23, 47, 79} and f : A → B, g : B → C be defined as f(x) = 2x + 1 and g(x) = x2 − 2. Express (gof)−1 and f−1 og−1 as the sets of ordered pairs and verify that (gof)−1 = f−1 og−1.
Consider f : R → R given by f(x) = 4x + 3. Show that f is invertible. Find the inverse of f.
Let A = R - {3} and B = R - {1}. Consider the function f : A → B defined by f(x) = `(x-2)/(x-3).`Show that f is one-one and onto and hence find f-1.
[CBSE 2012, 2014]
Consider the function f : R+ → [-9 , ∞ ]given by f(x) = 5x2 + 6x - 9. Prove that f is invertible with f -1 (y) = `(sqrt(54 + 5y) -3)/5` [CBSE 2015]
Write the total number of one-one functions from set A = {1, 2, 3, 4} to set B = {a, b, c}.
If f : R → R is defined by f(x) = 10 x − 7, then write f−1 (x).
Let \[f : \left( - \frac{\pi}{2}, \frac{\pi}{2} \right) \to R\] be a function defined by f(x) = cos [x]. Write range (f).
Let f : R − {−1} → R − {1} be given by\[f\left( x \right) = \frac{x}{x + 1} . \text{Write } f^{- 1} \left( x \right)\]
If f(x) = x + 7 and g(x) = x − 7, x ∈ R, write fog (7).
If f : R → R be defined by f(x) = (3 − x3)1/3, then find fof (x).
The range of the function
\[f\left( x \right) =^{7 - x} P_{x - 3}\]
Which of the following functions form Z to itself are bijections?
Let
\[A = \left\{ x : - 1 \leq x \leq 1 \right\} \text{and} f : A \to \text{A such that f}\left( x \right) = x|x|\]
Let
\[f : R \to R\] be a function defined by
Let
\[f : R - \left\{ n \right\} \to R\]
\[f : R \to R\] is defined by
\[f\left( x \right) = \frac{e^{x^2} - e^{- x^2}}{e^{x^2 + e^{- x^2}}} is\]
Let \[f\left( x \right) = \frac{\alpha x}{x + 1}, x \neq - 1\] Then, for what value of α is \[f \left( f\left( x \right) \right) = x?\]
If \[f : R \to R\] is given by \[f\left( x \right) = x^3 + 3, \text{then} f^{- 1} \left( x \right)\] is equal to
Let
\[f : R \to R\] be given by \[f\left( x \right) = x^2 - 3\] Then, \[f^{- 1}\] is given by
Which function is used to check whether a character is alphanumeric or not?
Write about strcmp() function.
Let the function f: R → R be defined by f(x) = 4x – 1, ∀ x ∈ R. Then, show that f is one-one.
If the set A contains 5 elements and the set B contains 6 elements, then the number of one-one and onto mappings from A to B is ______.
Let f: R → R be the functions defined by f(x) = x3 + 5. Then f–1(x) is ______.
Let f : R → R be defind by f(x) = `1/"x" AA "x" in "R".` Then f is ____________.
Let g(x) = x2 – 4x – 5, then ____________.
Function f: R → R, defined by f(x) = `x/(x^2 + 1)` ∀ x ∈ R is not
If log102 = 0.3010.log103 = 0.4771 then the number of ciphers after decimal before a significant figure comes in `(5/3)^-100` is ______.
Difference between the greatest and least value of f(x) = `(1 + (cos^-1x)/π)^2 - (1 + (sin^-1x)/π)^2` is ______.
Which one of the following graphs is a function of x?
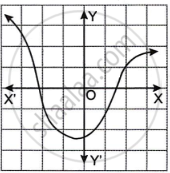 |
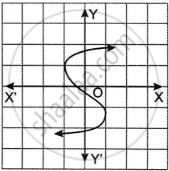 |
| Graph A | Graph B |
