Advertisements
Advertisements
Question
Let A = R – {2} and B = R – {1}. If f: A `→` B is a function defined by f(x) = `(x - 1)/(x - 2)` then show that f is a one-one and an onto function.
Solution
Let A = R – {2}, B = R – {1}
f: A `→` B s.t. f(x) = `(x - 1)/(x - 2)`
For x1, x2 ∈ A
f(x1) = f(x2)
`\implies (x_1 - 1)/(x_1 - 2) = (x_2 - 1)/(x_2 - 2)`
`\implies (x_1 - 1)/(x_1 - 2) - 1 = (x_2 - 1)/(x_2 - 2) - 1`
`\implies 1/(x_1 - 2) = 1/(x_2 - 2)`
`\implies` x1 – 2 = x2 – 2
`\implies` x1 = x2
∴ f(x) is one-one function.
Also if f(x) = y, where y ∈ B.
`\implies (x - 1)/(x - 2)` = y
`\implies` x – 1 = xy – 2y
`\implies` 2y – 1 = xy – x
`\implies` 2y – 1 = x(y – 1)
x = `(2y - 1)/(y - 1) ∈ A`
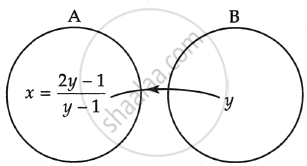
Clearly every element y ∈ B is associated to x = `(2y - 1)/(y - 1)` of set A.
So Range of f = B `\implies` f is into
Hence f is one-one and onto function.
APPEARS IN
RELATED QUESTIONS
Let f: N → N be defined by f(n) = `{((n+1)/2, ",if n is odd"),(n/2,",n is even"):}` for all n ∈ N.
State whether the function f is bijective. Justify your answer.
Let f: R → R be defined as f(x) = 10x + 7. Find the function g: R → R such that g o f = f o g = 1R.
Give an example of a function which is neither one-one nor onto ?
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = x3 + 1
Find the number of all onto functions from the set A = {1, 2, 3, ..., n} to itself.
Find fog and gof if : f(x) = `x^2` + 2 , g (x) = 1 − `1/ (1-x)`.
If f(x) = 2x + 5 and g(x) = x2 + 1 be two real functions, then describe each of the following functions:
(1) fog
(2) gof
(3) fof
(4) f2
Also, show that fof ≠ f2
State with reason whether the following functions have inverse:
h : {2, 3, 4, 5} → {7, 9, 11, 13} with h = {(2, 7), (3, 9), (4, 11), (5, 13)}
If f : Q → Q, g : Q → Q are two functions defined by f(x) = 2 x and g(x) = x + 2, show that f and g are bijective maps. Verify that (gof)−1 = f−1 og −1.
Let `f : R - {- 3/5}` → R be a function defined as `f (x) = (2x)/(5x +3).`
f-1 : Range of f → `R -{-3/5}`.
\[f : A \to \text{B given by } 3^{ f\left( x \right)} + 2^{- x} = 4\] is a bijection, then
Which of the following functions from
to itself are bijections?
The function \[f : R \to R\] defined by
\[f\left( x \right) = 6^x + 6^{|x|}\] is
Let \[f\left( x \right) = x^2 and g\left( x \right) = 2^x\] Then, the solution set of the equation
The distinct linear functions that map [−1, 1] onto [0, 2] are
Let f, g: R → R be two functions defined as f(x) = |x| + x and g(x) = x – x ∀ x ∈ R. Then, find f o g and g o f
Let R be the set of real numbers and f: R → R be the function defined by f(x) = 4x + 5. Show that f is invertible and find f–1.
Let X = {1, 2, 3}and Y = {4, 5}. Find whether the following subset of X ×Y are function from X to Y or not
g = {(1, 4), (2, 4), (3, 4)}
Let A = [–1, 1]. Then, discuss whether the following functions defined on A are one-one, onto or bijective:
h(x) = x|x|
Let A = [–1, 1]. Then, discuss whether the following functions defined on A are one-one, onto or bijective:
k(x) = x2
Let A = {1, 2, 3, ...n} and B = {a, b}. Then the number of surjections from A into B is ______.
The function f: R → R defined as f(x) = x3 is:
Let f: R → R defined by f(x) = x4. Choose the correct answer
The domain of the function `cos^-1((2sin^-1(1/(4x^2-1)))/π)` is ______.
Let [x] denote the greatest integer ≤ x, where x ∈ R. If the domain of the real valued function f(x) = `sqrt((|[x]| - 2)/(|[x]| - 3)` is (–∞, a) ∪ [b, c) ∪ [4, ∞), a < b < c, then the value of a + b + c is ______.
If log102 = 0.3010.log103 = 0.4771 then the number of ciphers after decimal before a significant figure comes in `(5/3)^-100` is ______.
Let f(n) = `[1/3 + (3n)/100]n`, where [n] denotes the greatest integer less than or equal to n. Then `sum_(n = 1)^56f(n)` is equal to ______.
Find the domain of sin–1 (x2 – 4).
The trigonometric equation tan–1x = 3tan–1 a has solution for ______.
