Advertisements
Advertisements
Question
Find the domain of sin–1 (x2 – 4).
Solution
–1 ≤ (x2 – 4) ≤ 1
`\implies` 3 ≤ x2 ≤ 5
`\implies sqrt(3) ≤ |x| ≤ sqrt(5)`
`\implies x ∈ [-sqrt(5), -sqrt(3)] ∪ [sqrt(3), sqrt(5)]`.
So required domain is `[-sqrt(5), -sqrt(3)] ∪ [sqrt(3), sqrt(5)]`.
APPEARS IN
RELATED QUESTIONS
Check the injectivity and surjectivity of the following function:
f: N → N given by f(x) = x2
Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from A to B. Show that f is one-one.
Which of the following functions from A to B are one-one and onto ?
f3 = {(a, x), (b, x), (c, z), (d, z)} ; A = {a, b, c, d,}, B = {x, y, z}.
Classify the following function as injection, surjection or bijection : f : N → N given by f(x) = x2
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = |x|
Let A = [-1, 1]. Then, discuss whether the following functions from A to itself is one-one, onto or bijective : h(x) = x2
Find fog (2) and gof (1) when : f : R → R ; f(x) = x2 + 8 and g : R → R; g(x) = 3x3 + 1.
State with reason whether the following functions have inverse :
f : {1, 2, 3, 4} → {10} with f = {(1, 10), (2, 10), (3, 10), (4, 10)}
If f : R → R be defined by f(x) = x3 −3, then prove that f−1 exists and find a formula for f−1. Hence, find f−1(24) and f−1 (5).
Let A = {x &epsis; R | −1 ≤ x ≤ 1} and let f : A → A, g : A → A be two functions defined by f(x) = x2 and g(x) = sin (π x/2). Show that g−1 exists but f−1 does not exist. Also, find g−1.
If f : A → A, g : A → A are two bijections, then prove that fog is a surjection ?
Let \[f : \left( - \frac{\pi}{2}, \frac{\pi}{2} \right) \to R\] be a function defined by f(x) = cos [x]. Write range (f).
If f : R → R is defined by f(x) = 3x + 2, find f (f (x)).
Let the function
\[f : R - \left\{ - b \right\} \to R - \left\{ 1 \right\}\]
\[f\left( x \right) = \frac{x + a}{x + b}, a \neq b .\text{Then},\]
\[f : R \to R\] is defined by
\[f\left( x \right) = \frac{e^{x^2} - e^{- x^2}}{e^{x^2 + e^{- x^2}}} is\]
The function
Mark the correct alternative in the following question:
Let A = {1, 2, ... , n} and B = {a, b}. Then the number of subjections from A into B is
Set A has 3 elements and the set B has 4 elements. Then the number of injective mappings that can be defined from A to B is ______.
Let C be the set of complex numbers. Prove that the mapping f: C → R given by f(z) = |z|, ∀ z ∈ C, is neither one-one nor onto.
Let X = {1, 2, 3}and Y = {4, 5}. Find whether the following subset of X ×Y are function from X to Y or not
f = {(1, 4), (1, 5), (2, 4), (3, 5)}
If the set A contains 5 elements and the set B contains 6 elements, then the number of one-one and onto mappings from A to B is ______.
Let f: R → R be given by f(x) = tan x. Then f–1(1) is ______.
The function f : A → B defined by f(x) = 4x + 7, x ∈ R is ____________.
Let X = {-1, 0, 1}, Y = {0, 2} and a function f : X → Y defiend by y = 2x4, is ____________.
If f: R → R given by f(x) =(3 − x3)1/3, find f0f(x)
Let f: R → R defined by f(x) = x4. Choose the correct answer
Let f: R → R defined by f(x) = 3x. Choose the correct answer
A function f: x → y is/are called onto (or surjective) if x under f.
Which one of the following graphs is a function of x?
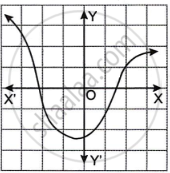 |
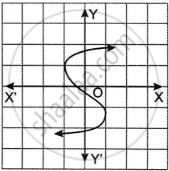 |
| Graph A | Graph B |
