Advertisements
Advertisements
प्रश्न
Find the domain of sin–1 (x2 – 4).
उत्तर
–1 ≤ (x2 – 4) ≤ 1
`\implies` 3 ≤ x2 ≤ 5
`\implies sqrt(3) ≤ |x| ≤ sqrt(5)`
`\implies x ∈ [-sqrt(5), -sqrt(3)] ∪ [sqrt(3), sqrt(5)]`.
So required domain is `[-sqrt(5), -sqrt(3)] ∪ [sqrt(3), sqrt(5)]`.
APPEARS IN
संबंधित प्रश्न
Prove that the greatest integer function f: R → R, given by f(x) = [x], is neither one-one nor onto, where [x] denotes the greatest integer less than or equal to x.
Classify the following function as injection, surjection or bijection : f : Z → Z given by f(x) = x3
Show that if f1 and f2 are one-one maps from R to R, then the product f1 × f2 : R → R defined by (f1 × f2) (x) = f1 (x) f2 (x) need not be one - one.
Find gof and fog when f : R → R and g : R → R is defined by f(x) = 2x + 3 and g(x) = x2 + 5 .
Give examples of two functions f : N → N and g : N → N, such that gof is onto but f is not onto.
Find fog and gof if : f (x) = |x|, g (x) = sin x .
If f(x) = 2x + 5 and g(x) = x2 + 1 be two real functions, then describe each of the following functions:
(1) fog
(2) gof
(3) fof
(4) f2
Also, show that fof ≠ f2
Show that the function f : Q → Q, defined by f(x) = 3x + 5, is invertible. Also, find f−1
If f : R → R be defined by f(x) = x3 −3, then prove that f−1 exists and find a formula for f−1. Hence, find f−1(24) and f−1 (5).
Let f : R `{- 4/3} `- 43 →">→ R be a function defined as f(x) = `(4x)/(3x +4)` . Show that f : R - `{-4/3}`→ Rang (f) is one-one and onto. Hence, find f -1.
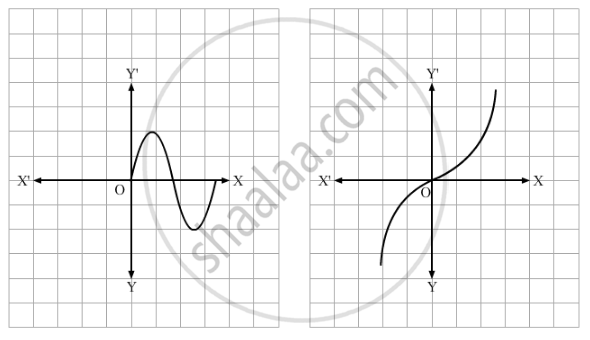
Which of the following graphs represents a one-one function?
If A = {a, b, c} and B = {−2, −1, 0, 1, 2}, write the total number of one-one functions from A to B.
If f : C → C is defined by f(x) = (x − 2)3, write f−1 (−1).
If f : R → R is defined by f(x) = 10 x − 7, then write f−1 (x).
Let A = {x ∈ R : −4 ≤ x ≤ 4 and x ≠ 0} and f : A → R be defined by \[f\left( x \right) = \frac{\left| x \right|}{x}\]Write the range of f.
If f : R → R be defined by f(x) = (3 − x3)1/3, then find fof (x).
If a function\[f : [2, \infty )\text{ to B defined by f}\left( x \right) = x^2 - 4x + 5\] is a bijection, then B =
The function f : [-1/2, 1/2, 1/2] → [-π /2,π/2], defined by f (x) = `sin^-1` (3x - `4x^3`), is
The inverse of the function
\[f : R \to \left\{ x \in R : x < 1 \right\}\] given by
\[f\left( x \right) = \frac{e^x - e^{- x}}{e^x + e^{- x}}\] is
Let
\[A = \left\{ x \in R : x \geq 1 \right\}\] The inverse of the function,
\[f : A \to A\] given by
\[f\left( x \right) = 2^{x \left( x - 1 \right)} , is\]
Let the function f: R → R be defined by f(x) = 4x – 1, ∀ x ∈ R. Then, show that f is one-one.
If A = {a, b, c, d} and f = {a, b), (b, d), (c, a), (d, c)}, show that f is one-one from A onto A. Find f–1
Are the following set of ordered pairs functions? If so, examine whether the mapping is injective or surjective.
{(x, y): x is a person, y is the mother of x}
Let X = {1, 2, 3}and Y = {4, 5}. Find whether the following subset of X ×Y are function from X to Y or not
g = {(1, 4), (2, 4), (3, 4)}
The function f : R → R given by f(x) = x3 – 1 is ____________.
Range of `"f"("x") = sqrt((1 - "cos x") sqrt ((1 - "cos x")sqrt ((1 - "cos x")....infty))`
Raji visited the Exhibition along with her family. The Exhibition had a huge swing, which attracted many children. Raji found that the swing traced the path of a Parabola as given by y = x2.
Answer the following questions using the above information.
- Let f: {1,2,3,....} → {1,4,9,....} be defined by f(x) = x2 is ____________.
If f: R → R given by f(x) =(3 − x3)1/3, find f0f(x)
Let f: R→R be defined as f(x) = 2x – 1 and g: R – {1}→R be defined as g(x) = `(x - 1/2)/(x - 1)`. Then the composition function f (g(x)) is ______.
If A = {x ∈ R: |x – 2| > 1}, B = `{x ∈ R : sqrt(x^2 - 3) > 1}`, C = {x ∈ R : |x – 4| ≥ 2} and Z is the set of all integers, then the number of subsets of the set (A ∩ B ∩ C) C ∩ Z is ______.
