Advertisements
Advertisements
प्रश्न
If f : R → R be defined by f(x) = x3 −3, then prove that f−1 exists and find a formula for f−1. Hence, find f−1(24) and f−1 (5).
उत्तर
Injectivity of f :
Let x and y be two elements in domain (R),
such that, x3 − 3 = y3 − 3
⇒ x3 = y3
⇒ x = y
So, f is one-one.
Surjectivity of f :
Let y be in the co-domain (R) such that f(x) = y
⇒ x3 - 3 = y
⇒ x3 = y + 3
⇒ `x = 3sqrt(y+3) in R`
⇒ f is onto.
So, f is a bijection and, hence, it is invertible.
Finding f -1:
Let f−1(x) = y ...(1)
⇒ x= f( y)
⇒ x = y3−3
⇒ x + 3 = y3
⇒ `y = 3sqrt(x+3) = f^-1 (x)` [from (1)]
`So, f^-1 (x) = 3sqrt(x+3)`
Now`, f^1 (24) = 3sqrt(24+3) = 3sqrt27 = 3sqrt3^3 =3`
and `f^-1 (5) = 3sqrt(5+3) = 3 sqrt8 = 3sqrt2^3 =2`
APPEARS IN
संबंधित प्रश्न
Following the case, state whether the function is one-one, onto, or bijective. Justify your answer.
f: R → R defined by f(x) = 1 + x2
Let f: N → N be defined by f(n) = `{((n+1)/2, ",if n is odd"),(n/2,",n is even"):}` for all n ∈ N.
State whether the function f is bijective. Justify your answer.
Let f: R → R be defined as f(x) = x4. Choose the correct answer.
Find the number of all onto functions from the set {1, 2, 3, …, n} to itself.
Classify the following function as injection, surjection or bijection : f : Z → Z given by f(x) = x2
Classify the following function as injection, surjection or bijection : f : Z → Z given by f(x) = x3
Classify the following function as injection, surjection or bijection :
f : Z → Z, defined by f(x) = x − 5
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = 5x3 + 4
If f : A → B is an injection, such that range of f = {a}, determine the number of elements in A.
Find fog (2) and gof (1) when : f : R → R ; f(x) = x2 + 8 and g : R → R; g(x) = 3x3 + 1.
Find fog and gof if : f (x) = |x|, g (x) = sin x .
Find fog and gof if : f (x) = x+1, g (x) = sin x .
Find fog and gof if : f(x) = c, c ∈ R, g(x) = sin `x^2`
State with reason whether the following functions have inverse :
f : {1, 2, 3, 4} → {10} with f = {(1, 10), (2, 10), (3, 10), (4, 10)}
Let A = {x &epsis; R | −1 ≤ x ≤ 1} and let f : A → A, g : A → A be two functions defined by f(x) = x2 and g(x) = sin (π x/2). Show that g−1 exists but f−1 does not exist. Also, find g−1.
If f : A → A, g : A → A are two bijections, then prove that fog is a surjection ?
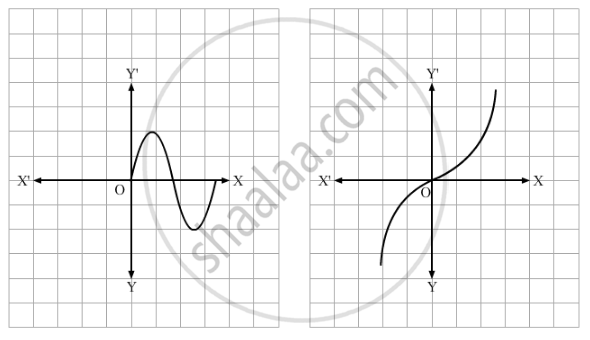
Which of the following graphs represents a one-one function?
If f : R → R, g : R → are given by f(x) = (x + 1)2 and g(x) = x2 + 1, then write the value of fog (−3).
Let `f : R - {- 3/5}` → R be a function defined as `f (x) = (2x)/(5x +3).`
f-1 : Range of f → `R -{-3/5}`.
Let f be an invertible real function. Write ( f-1 of ) (1) + ( f-1 of ) (2) +..... +( f-1 of ) (100 )
Write the domain of the real function f defined by f(x) = `sqrt (25 -x^2)` [NCERT EXEMPLAR]
If the mapping f : {1, 3, 4} → {1, 2, 5} and g : {1, 2, 5} → {1, 3}, given by f = {(1, 2), (3, 5), (4, 1)} and g = {(2, 3), (5, 1), (1, 3)}, then write fog. [NCERT EXEMPLAR]
A function f from the set of natural numbers to the set of integers defined by
\[f\left( n \right)\begin{cases}\frac{n - 1}{2}, & \text{when n is odd} \\ - \frac{n}{2}, & \text{when n is even}\end{cases}\]
Let \[f\left( x \right) = \frac{\alpha x}{x + 1}, x \neq - 1\] Then, for what value of α is \[f \left( f\left( x \right) \right) = x?\]
If \[f : R \to R\] is given by \[f\left( x \right) = x^3 + 3, \text{then} f^{- 1} \left( x \right)\] is equal to
Let N be the set of natural numbers and the function f: N → N be defined by f(n) = 2n + 3 ∀ n ∈ N. Then f is ______.
Let D be the domain of the real valued function f defined by f(x) = `sqrt(25 - x^2)`. Then, write D
Let the function f: R → R be defined by f(x) = cosx, ∀ x ∈ R. Show that f is neither one-one nor onto
The function f : R → R defined by f(x) = 3 – 4x is ____________.
Let f : R → R be a function defined by f(x) `= ("e"^abs"x" - "e"^-"x")/("e"^"x" + "e"^-"x")` then f(x) is
Range of `"f"("x") = sqrt((1 - "cos x") sqrt ((1 - "cos x")sqrt ((1 - "cos x")....infty))`
Let R be a relation on the set L of lines defined by l1 R l2 if l1 is perpendicular to l2, then relation R is ____________.
A general election of Lok Sabha is a gigantic exercise. About 911 million people were eligible to vote and voter turnout was about 67%, the highest ever

Let I be the set of all citizens of India who were eligible to exercise their voting right in the general election held in 2019. A relation ‘R’ is defined on I as follows:
R = {(V1, V2) ∶ V1, V2 ∈ I and both use their voting right in the general election - 2019}
- Mr. ’X’ and his wife ‘W’ both exercised their voting right in the general election-2019, Which of the following is true?
Consider a function f: `[0, pi/2] ->` R, given by f(x) = sinx and `g[0, pi/2] ->` R given by g(x) = cosx then f and g are
Let [x] denote the greatest integer ≤ x, where x ∈ R. If the domain of the real valued function f(x) = `sqrt((|[x]| - 2)/(|[x]| - 3)` is (–∞, a) ∪ [b, c) ∪ [4, ∞), a < b < c, then the value of a + b + c is ______.
Let f(x) = ax (a > 0) be written as f(x) = f1(x) + f2(x), where f1(x) is an even function and f2(x) is an odd function. Then f1(x + y) + f1(x – y) equals ______.
ASSERTION (A): The relation f : {1, 2, 3, 4} `rightarrow` {x, y, z, p} defined by f = {(1, x), (2, y), (3, z)} is a bijective function.
REASON (R): The function f : {1, 2, 3} `rightarrow` {x, y, z, p} such that f = {(1, x), (2, y), (3, z)} is one-one.
Let A = R – {2} and B = R – {1}. If f: A `→` B is a function defined by f(x) = `(x - 1)/(x - 2)` then show that f is a one-one and an onto function.
