Advertisements
Advertisements
प्रश्न
Which of the following graphs represents a one-one function?
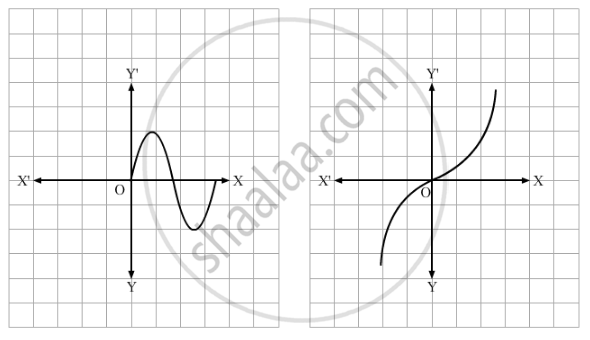
उत्तर
APPEARS IN
संबंधित प्रश्न
Given examples of two functions f: N → N and g: N → N such that gof is onto but f is not onto.
(Hint: Consider f(x) = x + 1 and `g(x) = {(x-1, ifx >1),(1, if x = 1):}`
Classify the following function as injection, surjection or bijection :
f : Q − {3} → Q, defined by `f (x) = (2x +3)/(x-3)`
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = 3 − 4x
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = 1 + x2
If f : A → B is an injection, such that range of f = {a}, determine the number of elements in A.
Find gof and fog when f : R → R and g : R → R is defined by f(x) = 2x + x2 and g(x) = x3
Let f = {(3, 1), (9, 3), (12, 4)} and g = {(1, 3), (3, 3) (4, 9) (5, 9)}. Show that gof and fog are both defined. Also, find fog and gof.
Let f : R → R and g : R → R be defined by f(x) = x2 and g(x) = x + 1. Show that fog ≠ gof.
Find fog and gof if : f(x)= x + 1, g (x) = 2x + 3 .
Let f, g, h be real functions given by f(x) = sin x, g (x) = 2x and h (x) = cos x. Prove that fog = go (fh).
` if f : (-π/2 , π/2)` → R and g : [−1, 1]→ R be defined as f(x) = tan x and g(x) = `sqrt(1 - x^2)` respectively, describe fog and gof.
Let f be a real function given by f (x)=`sqrt (x-2)`
Find each of the following:
(i) fof
(ii) fofof
(iii) (fofof) (38)
(iv) f2
Also, show that fof ≠ `f^2` .
Let
f (x) =`{ (1 + x, 0≤ x ≤ 2) , (3 -x , 2 < x ≤ 3):}`
Find fof.
Consider f : R+ → [−5, ∞) given by f(x) = 9x2 + 6x − 5. Show that f is invertible with `f^-1 (x) = (sqrt (x +6)-1)/3 .`
Write the total number of one-one functions from set A = {1, 2, 3, 4} to set B = {a, b, c}.
If f : R → R is defined by f(x) = x2, write f−1 (25)
If f : C → C is defined by f(x) = x2, write f−1 (−4). Here, C denotes the set of all complex numbers.
Let C denote the set of all complex numbers. A function f : C → C is defined by f(x) = x3. Write f−1(1).
Let \[f : \left( - \frac{\pi}{2}, \frac{\pi}{2} \right) \to R\] be a function defined by f(x) = cos [x]. Write range (f).
Let A = {x ∈ R : −4 ≤ x ≤ 4 and x ≠ 0} and f : A → R be defined by \[f\left( x \right) = \frac{\left| x \right|}{x}\]Write the range of f.
Write the domain of the real function
`f (x) = sqrt([x] - x) .`
Let the function
\[f : R - \left\{ - b \right\} \to R - \left\{ 1 \right\}\]
\[f\left( x \right) = \frac{x + a}{x + b}, a \neq b .\text{Then},\]
Let
\[A = \left\{ x \in R : - 1 \leq x \leq 1 \right\} = B\] Then, the mapping\[f : A \to \text{B given by} f\left( x \right) = x\left| x \right|\] is
Let
f : R → R be given by
\[f\left( x \right) = \left[ x^2 \right] + \left[ x + 1 \right] - 3\]
where [x] denotes the greatest integer less than or equal to x. Then, f(x) is
(d) one-one and onto
Let M be the set of all 2 × 2 matrices with entries from the set R of real numbers. Then, the function f : M→ R defined by f(A) = |A| for every A ∈ M, is
The function f : [-1/2, 1/2, 1/2] → [-π /2,π/2], defined by f (x) = `sin^-1` (3x - `4x^3`), is
\[f : Z \to Z\] be given by
` f (x) = {(x/2, ", if x is even" ) ,(0 , ", if x is odd "):}`
Then, f is
If \[F : [1, \infty ) \to [2, \infty )\] is given by
\[f\left( x \right) = x + \frac{1}{x}, then f^{- 1} \left( x \right)\]
Let
\[f : [2, \infty ) \to X\] be defined by
\[f\left( x \right) = 4x - x^2\] Then, f is invertible if X =
Let f : R → R be a function defined by f(x) `= ("e"^abs"x" - "e"^-"x")/("e"^"x" + "e"^-"x")` then f(x) is
Let g(x) = x2 – 4x – 5, then ____________.
If N be the set of all-natural numbers, consider f: N → N such that f(x) = 2x, ∀ x ∈ N, then f is ____________.
Range of `"f"("x") = sqrt((1 - "cos x") sqrt ((1 - "cos x")sqrt ((1 - "cos x")....infty))`
An organization conducted a bike race under 2 different categories-boys and girls. Totally there were 250 participants. Among all of them finally, three from Category 1 and two from Category 2 were selected for the final race. Ravi forms two sets B and G with these participants for his college project. Let B = {b1,b2,b3} G={g1,g2} where B represents the set of boys selected and G the set of girls who were selected for the final race.
Ravi decides to explore these sets for various types of relations and functions.
- Let R: B → G be defined by R = { (b1,g1), (b2,g2),(b3,g1)}, then R is ____________.
A function f: x → y is/are called onto (or surjective) if x under f.
Function f: R → R, defined by f(x) = `x/(x^2 + 1)` ∀ x ∈ R is not
`x^(log_5x) > 5` implies ______.
Let f: R→R be a polynomial function satisfying f(x + y) = f(x) + f(y) + 3xy(x + y) –1 ∀ x, y ∈ R and f'(0) = 1, then `lim_(x→∞)(f(2x))/(f(x)` is equal to ______.
The trigonometric equation tan–1x = 3tan–1 a has solution for ______.
