Advertisements
Advertisements
Question
The function \[f : R \to R\] defined by
\[f\left( x \right) = 6^x + 6^{|x|}\] is
Options
one-one and onto
many one and onto
one-one and into
many one and into
Solution
(d) many one and into
Graph of the given function is as follows :
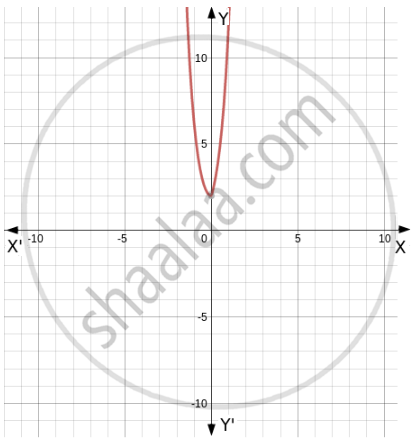
A line parallel to X axis is cutting the graph at two different values.
Therefore, for two different values of x we are getting the same value of y .
That means it is many one function .
From the given graph we can see that the range is
\[[2, \infty )\]b
and R is the codomain of the given function .
Hence, Codomain
\[\neq\] Range
Therefore, the given function is into .
APPEARS IN
RELATED QUESTIONS
Show that the function f: R* → R* defined by `f(x) = 1/x` is one-one and onto, where R* is the set of all non-zero real numbers. Is the result true if the domain R* is replaced by N, with co-domain being same as R?
Show that the function f: R → R given by f(x) = x3 is injective.
Given examples of two functions f: N → N and g: N → N such that gof is onto but f is not onto.
(Hint: Consider f(x) = x + 1 and `g(x) = {(x-1, ifx >1),(1, if x = 1):}`
Find the number of all onto functions from the set {1, 2, 3, …, n} to itself.
Classify the following function as injection, surjection or bijection : f : Z → Z given by f(x) = x2
Classify the following function as injection, surjection or bijection : f : N → N given by f(x) = x3
Set of ordered pair of a function? If so, examine whether the mapping is injective or surjective :{(x, y) : x is a person, y is the mother of x}
Let A = {1, 2, 3}. Write all one-one from A to itself.
If f : R → R be the function defined by f(x) = 4x3 + 7, show that f is a bijection.
Let f = {(1, −1), (4, −2), (9, −3), (16, 4)} and g = {(−1, −2), (−2, −4), (−3, −6), (4, 8)}. Show that gof is defined while fog is not defined. Also, find gof.
Let A = {a, b, c}, B = {u v, w} and let f and g be two functions from A to B and from B to A, respectively, defined as :
f = {(a, v), (b, u), (c, w)}, g = {(u, b), (v, a), (w, c)}.
Show that f and g both are bijections and find fog and gof.
Find fog and gof if : f (x) = |x|, g (x) = sin x .
State with reason whether the following functions have inverse :
g : {5, 6, 7, 8} → {1, 2, 3, 4} with g = {(5, 4), (6, 3), (7, 4), (8, 2)}
Consider f : {1, 2, 3} → {a, b, c} and g : {a, b, c} → {apple, ball, cat} defined as f (1) = a, f (2) = b, f (3) = c, g (a) = apple, g (b) = ball and g (c) = cat. Show that f, g and gof are invertible. Find f−1, g−1 and gof−1and show that (gof)−1 = f −1o g−1
Let A = {x &epsis; R | −1 ≤ x ≤ 1} and let f : A → A, g : A → A be two functions defined by f(x) = x2 and g(x) = sin (π x/2). Show that g−1 exists but f−1 does not exist. Also, find g−1.
If f : R → R is defined by f(x) = x2, write f−1 (25)
If f : R → R is given by f(x) = x3, write f−1 (1).
If f(x) = x + 7 and g(x) = x − 7, x ∈ R, write fog (7).
Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from A to B. State whether f is one-one or not.
Let f, g : R → R be defined by f(x) = 2x + l and g(x) = x2−2 for all x
∈ R, respectively. Then, find gof. [NCERT EXEMPLAR]
If a function g = {(1, 1), (2, 3), (3, 5), (4, 7)} is described by g(x) = \[\alpha x + \beta\] then find the values of \[\alpha\] and \[ \beta\] . [NCERT EXEMPLAR]
Let M be the set of all 2 × 2 matrices with entries from the set R of real numbers. Then, the function f : M→ R defined by f(A) = |A| for every A ∈ M, is
Let [x] denote the greatest integer less than or equal to x. If \[f\left( x \right) = \sin^{- 1} x, g\left( x \right) = \left[ x^2 \right]\text{ and } h\left( x \right) = 2x, \frac{1}{2} \leq x \leq \frac{1}{\sqrt{2}}\]
Mark the correct alternative in the following question:
Let f : R → R be given by f(x) = tanx. Then, f-1(1) is
The domain of the function f: R → R defined by f(x) = `sqrt(x^2 - 3x + 2)` is ______
Let X = {1, 2, 3}and Y = {4, 5}. Find whether the following subset of X ×Y are function from X to Y or not
g = {(1, 4), (2, 4), (3, 4)}
Let f: R → R be the functions defined by f(x) = x3 + 5. Then f–1(x) is ______.
Let f: `[2, oo)` → R be the function defined by f(x) = x2 – 4x + 5, then the range of f is ______.
Which of the following functions from Z into Z is bijective?
Let f : R `->` R be a function defined by f(x) = x3 + 4, then f is ______.
A general election of Lok Sabha is a gigantic exercise. About 911 million people were eligible to vote and voter turnout was about 67%, the highest ever

Let I be the set of all citizens of India who were eligible to exercise their voting right in the general election held in 2019. A relation ‘R’ is defined on I as follows:
R = {(V1, V2) ∶ V1, V2 ∈ I and both use their voting right in the general election - 2019}
- Mr. ’X’ and his wife ‘W’ both exercised their voting right in the general election-2019, Which of the following is true?
If `f : R -> R^+ U {0}` be defined by `f(x) = x^2, x ∈ R`. The mapping is
If f; R → R f(x) = 10x + 3 then f–1(x) is:
The graph of the function y = f(x) is symmetrical about the line x = 2, then ______.
Let S = {1, 2, 3, 4, 5, 6, 7}. Then the number of possible functions f: S `rightarrow` S such that f(m.n) = f(m).f(n) for every m, n ∈ S and m.n ∈ S is equal to ______.
A function f : [– 4, 4] `rightarrow` [0, 4] is given by f(x) = `sqrt(16 - x^2)`. Show that f is an onto function but not a one-one function. Further, find all possible values of 'a' for which f(a) = `sqrt(7)`.
Write the domain and range (principle value branch) of the following functions:
f(x) = tan–1 x.
Find the domain of sin–1 (x2 – 4).
