Advertisements
Advertisements
Question
Find fog and gof if : f (x) = |x|, g (x) = sin x .
Solution
f (x) = |x|, g(x) = sin x
f : R → (0, ∞) ; g : R→[−1, 1]
Computing fog:
Clearly, the range of g is a subset of the domain of f.
⇒ fog : R→R
(fog) (x) = f (g (x))
= f (sin x)
= |sin x|
Computing gof:
Clearly, the range of f is a subset of the domain of g.
⇒ fog : R→ R
(gof) (x) = g (f (x))
= g (|x|)
= sin |x|
APPEARS IN
RELATED QUESTIONS
Let f: N → N be defined by f(n) = `{((n+1)/2, ",if n is odd"),(n/2,",n is even"):}` for all n ∈ N.
State whether the function f is bijective. Justify your answer.
Let f: R → R be defined as f(x) = x4. Choose the correct answer.
Give an example of a function which is neither one-one nor onto ?
Let A = [-1, 1]. Then, discuss whether the following function from A to itself is one-one, onto or bijective : g(x) = |x|
Let A = [-1, 1]. Then, discuss whether the following functions from A to itself is one-one, onto or bijective : h(x) = x2
Set of ordered pair of a function? If so, examine whether the mapping is injective or surjective :{(x, y) : x is a person, y is the mother of x}
Let f : N → N be defined by
`f(n) = { (n+ 1, if n is odd),( n-1 , if n is even):}`
Show that f is a bijection.
[CBSE 2012, NCERT]
Find fog and gof if : f(x) = c, c ∈ R, g(x) = sin `x^2`
Consider the function f : R+ → [-9 , ∞ ]given by f(x) = 5x2 + 6x - 9. Prove that f is invertible with f -1 (y) = `(sqrt(54 + 5y) -3)/5` [CBSE 2015]
Let A and B be two sets, each with a finite number of elements. Assume that there is an injective map from A to B and that there is an injective map from B to A. Prove that there is a bijection from A to B.
If f : A → A, g : A → A are two bijections, then prove that fog is a surjection ?
If f : C → C is defined by f(x) = x4, write f−1 (1).
If f : C → C is defined by f(x) = (x − 2)3, write f−1 (−1).
Let \[f : \left( - \frac{\pi}{2}, \frac{\pi}{2} \right) \to R\] be a function defined by f(x) = cos [x]. Write range (f).
Let \[f : \left[ - \frac{\pi}{2}, \frac{\pi}{2} \right] \to\] A be defined by f(x) = sin x. If f is a bijection, write set A.
Let `f : R - {- 3/5}` → R be a function defined as `f (x) = (2x)/(5x +3).`
f-1 : Range of f → `R -{-3/5}`.
Let f be an invertible real function. Write ( f-1 of ) (1) + ( f-1 of ) (2) +..... +( f-1 of ) (100 )
Write the domain of the real function
`f (x) = 1/(sqrt([x] - x)`.
Let the function
\[f : R - \left\{ - b \right\} \to R - \left\{ 1 \right\}\]
\[f\left( x \right) = \frac{x + a}{x + b}, a \neq b .\text{Then},\]
The function \[f : [0, \infty ) \to \text {R given by } f\left( x \right) = \frac{x}{x + 1} is\]
Let \[f\left( x \right) = \frac{1}{1 - x} . \text{Then}, \left\{ f o \left( fof \right) \right\} \left( x \right)\]
The distinct linear functions that map [−1, 1] onto [0, 2] are
Let
\[f : [2, \infty ) \to X\] be defined by
\[f\left( x \right) = 4x - x^2\] Then, f is invertible if X =
If \[f : R \to \left( - 1, 1 \right)\] is defined by
\[f\left( x \right) = \frac{- x|x|}{1 + x^2}, \text{ then } f^{- 1} \left( x \right)\] equals
Mark the correct alternative in the following question:
Let f : R → R be given by f(x) = tanx. Then, f-1(1) is
Let f: R → R be the function defined by f(x) = 4x – 3 ∀ x ∈ R. Then write f–1
Let R be the set of real numbers and f: R → R be the function defined by f(x) = 4x + 5. Show that f is invertible and find f–1.
Let X = {1, 2, 3}and Y = {4, 5}. Find whether the following subset of X ×Y are function from X to Y or not
g = {(1, 4), (2, 4), (3, 4)}
Let A = [–1, 1]. Then, discuss whether the following functions defined on A are one-one, onto or bijective:
f(x) = `x/2`
The function f : A → B defined by f(x) = 4x + 7, x ∈ R is ____________.
Let f : R → R be a function defined by f(x) `= ("e"^abs"x" - "e"^-"x")/("e"^"x" + "e"^-"x")` then f(x) is
Let A = R – {3}, B = R – {1}. Let f : A → B be defined by `"f"("x") = ("x" - 2)/("x" - 3)` Then, ____________.
Let n(A) = 4 and n(B) = 6, Then the number of one – one functions from 'A' to 'B' is:
If A = {x ∈ R: |x – 2| > 1}, B = `{x ∈ R : sqrt(x^2 - 3) > 1}`, C = {x ∈ R : |x – 4| ≥ 2} and Z is the set of all integers, then the number of subsets of the set (A ∩ B ∩ C) C ∩ Z is ______.
Let S = {1, 2, 3, 4, 5, 6, 7}. Then the number of possible functions f: S `rightarrow` S such that f(m.n) = f(m).f(n) for every m, n ∈ S and m.n ∈ S is equal to ______.
Let f(x) be a polynomial function of degree 6 such that `d/dx (f(x))` = (x – 1)3 (x – 3)2, then
Assertion (A): f(x) has a minimum at x = 1.
Reason (R): When `d/dx (f(x)) < 0, ∀ x ∈ (a - h, a)` and `d/dx (f(x)) > 0, ∀ x ∈ (a, a + h)`; where 'h' is an infinitesimally small positive quantity, then f(x) has a minimum at x = a, provided f(x) is continuous at x = a.
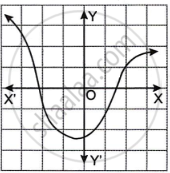
Which one of the following graphs is a function of x?
 |
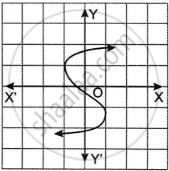 |
| Graph A | Graph B |
