RD Sharma solutions for Mathematics [English] Class 12 chapter 2 - Functions [Latest edition]

Give an example of a function which is one-one but not onto ?

Give an example of a function which is not one-one but onto ?

Give an example of a function which is neither one-one nor onto ?

Which of the following functions from A to B are one-one and onto?
 f₁ = {(1, 3), (2, 5), (3, 7)} ; A = {1, 2, 3}, B = {3, 5, 7}

Which of the following functions from A to B are one-one and onto?

 f₂ = {(2, a), (3, b), (4, c)} ; A = {2, 3, 4}, B = {a, b, c}

 Which of the following functions from A to B are one-one and onto ?  

f₃ = {(a, x), (b, x), (c, z), (d, z)} ; A = {a, b, c, d,}, B = {x, y, z}. 

Prove that the function f : N → N, defined by f(x) = x² + x + 1, is one-one but not onto

Let A = {−1, 0, 1} and f = {(x, x²) : x ∈ A}. Show that f : A → A is neither one-one nor onto.

Classify the following function as injection, surjection or bijection : f : N → N given by f(x) = x²

Classify the following function as injection, surjection or bijection :  f : Z → Z given by f(x) = x²

Classify the following function as injection, surjection or bijection : f : N → N given by f(x) = x³

Classify the following function as injection, surjection or bijection :  f : Z → Z given by f(x) = x³

Classify the following function as injection, surjection or bijection :

f : R → R, defined by f(x) = |x|

Classify the following function as injection, surjection or bijection :

f : Z → Z, defined by f(x) = x² + x

Classify the following function as injection, surjection or bijection :

 f : Z → Z, defined by f(x) = x − 5 

Classify the following function as injection, surjection or bijection :

 f : R → R, defined by f(x) = sinx

Classify the following function as injection, surjection or bijection :

f : R → R, defined by f(x) = x³ + 1

Classify the following function as injection, surjection or bijection :

 f : R → R, defined by f(x) = x³ − x

Classify the following function as injection, surjection or bijection :

f : R → R, defined by f(x) = sin²x + cos²x

Classify the following function as injection, surjection or bijection :

f : Q − {3} → Q, defined by `f (x) = (2x +3)/(x-3)`

Classify the following function as injection, surjection or bijection :

f : Q → Q, defined by f(x) = x³ + 1

Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = 5x³ + 4

Classify the following function as injection, surjection or bijection :

f : R → R, defined by f(x) = 3 − 4x

Classify the following function as injection, surjection or bijection :

f : R → R, defined by f(x) = 1 + x²

Classify the following function as injection, surjection or bijection :

f : R → R, defined by f(x) = `x/(x^2 +1)`

If f : A → B is an injection, such that range of f = {a}, determine the number of elements in A.

Show that the function f : R − {3} → R − {2} given by f(x) = `(x-2)/(x-3)` is a bijection.

Let A = [-1, 1]. Then, discuss whether the following function from A to itself is one-one, onto or bijective : `f (x) = x/2`

Let A = [-1, 1]. Then, discuss whether the following function from A to itself is one-one, onto or bijective : g(x) = |x|  

Let A = [-1, 1]. Then, discuss whether the following functions from A to itself is one-one, onto or bijective : h(x) = x² 

Set of ordered pair of  a function? If so, examine whether the mapping is injective or surjective :{(x, y) : x is a person, y is the mother of x}

Set of ordered pair of a function ? If so, examine whether the mapping is injective or surjective :{(a, b) : a is a person, b is an ancestor of a} 

Let A = {1, 2, 3}. Write all one-one from A to itself.

If f : R → R be the function defined by f(x) = 4x³ + 7, show that f is a bijection.

Show that the exponential function f : R → R, given by f(x) = e^x, is one-one but not onto. What happens if the co-domain is replaced by`R0^+` (set of all positive real numbers)?

Show that the logarithmic function  f : R0⁺ → R   given  by f (x)  log_a x ,a> 0   is   a  bijection.

If A = {1, 2, 3}, show that a one-one function f : A → A must be onto.

If A = {1, 2, 3}, show that a onto function f : A → A must be one-one.

Find the number of all onto functions from the set A = {1, 2, 3, ..., n} to itself.

Give examples of two one-one functions f₁ and f₂ from R to R, such that f₁ + f₂ : R → R. defined by (f₁ + f₂) (x) = f₁ (x) + f₂ (x) is not one-one.

Give examples of two surjective functions f₁ and f₂ from Z to Z such that f₁ + f₂ is not surjective.

Show that if f₁ and f₂ are one-one maps from R to R, then the product f₁ × f₂ : R → R defined by (f₁ × f₂) (x) = f₁ (x) f₂ (x) need not be one - one.

Suppose f₁ and f₂ are non-zero one-one functions from R to R. Is `f_1 / f^2` necessarily one - one? Justify your answer. Here,`f_1/f_2 : R → R   is   given   by   (f_1/f_2) (x) = (f_1(x))/(f_2 (x))  for all  x in R .`

Given A = {2, 3, 4}, B = {2, 5, 6, 7}. Construct an example of each of the following:
(i) an injective map from A to B
(ii) a mapping from A to B which is not injective
(iii) a mapping from A to B.

Show that f : R→ R, given by f(x) = x — [x], is neither one-one nor onto.

Let f : N → N be defined by

`f(n) = { (n+ 1, if n  is  odd),( n-1 , if n  is  even):}`

Show that f is a bijection. 

                      [CBSE 2012, NCERT]

Find gof and fog when f : R → R and g : R → R is defined by f(x) = 2x + 3 and  g(x) = x² + 5 .

Find fog and gof  if : f (x) = x2 g(x) = cos x .

Find gof and fog when f : R → R and g : R → R is defined by  f(x) = 2x + x² and  g(x) = x³

Find gof and fog when f : R → R and g : R → R is defined by  f(x) = x² + 8 and g(x) = 3x³ + 1 .

Find gof and fog when f : R → R and g : R → R is defined by  f(x) = x and g(x) = |x| .

 Find fog and gof  if  : f (x) = ex g(x) = loge x .

Find gof and fog when f : R → R and g : R → R is defined by  f(x) = x² + 2x − 3 and  g(x) = 3x − 4 .

Find gof and fog when f : R → R and g : R → R is  defined by  f(x) = 8x³ and  g(x) = x^1/3.

Let f = {(3, 1), (9, 3), (12, 4)} and g = {(1, 3), (3, 3) (4, 9) (5, 9)}. Show that gof and fog are both defined. Also, find fog and gof.

Let f = {(1, −1), (4, −2), (9, −3), (16, 4)} and g = {(−1, −2), (−2, −4), (−3, −6), (4, 8)}. Show that gof is defined while fog is not defined. Also, find gof.

Let A = {a, b, c}, B = {u v, w} and let f and g be two functions from A to B and from B to A, respectively, defined as :
f = {(a, v), (b, u), (c, w)}, g = {(u, b), (v, a), (w, c)}.
Show that f and g both are bijections and find fog and gof.

Find  fog (2) and gof (1) when : f : R → R ; f(x) = x² + 8 and g : R → R; g(x) = 3x³ + 1.

Let R⁺ be the set of all non-negative real numbers. If f : R⁺ → R⁺ and g : R⁺ → R⁺ are defined as `f(x)=x^2` and `g(x)=+sqrtx` , find fog and gof. Are they equal functions ?

Let f : R → R and g : R → R be defined by f(x) = x² and g(x) = x + 1. Show that fog ≠ gof.

Let f : R → R and g : R → R be defined by f(x) = x + 1 and g (x) = x − 1. Show that fog = gof = I_R.

Verify associativity for the following three mappings : f : N → Z₀ (the set of non-zero integers), g : Z₀ → Q and h : Q → R given by f(x) = 2x, g(x) = 1/x and h(x) = e^x.

Consider f : N → N, g : N → N and h : N → R defined as f(x) = 2x, g(y) = 3y + 4 and h(z) = sin z for all x, y, z ∈ N. Show that ho (gof) = (hog) of.

Give examples of two functions f : N → N and g : N → N, such that gof is onto but f is not onto.

Give examples of two functions f : N → Z and g : Z → Z, such that gof is injective but gis not injective.

If f : A → B and g : B → C are one-one functions, show that gof is a one-one function.

If f : A → B and g : B → C are onto functions, show that gof is a onto function.

Find fog and gof  if : f (x) = |x|, g (x) = sin x .

Find fog and gof  if : f (x) = x+1, g(x) = `e^x`

.

Find fog and gof  if : f(x) = sin⁻¹ x, g(x) = x²

Find fog and gof  if : f (x) = x+1, g (x) = sin x .

Find fog and gof  if : f(x)= x + 1, g (x) = 2x + 3 .

Find fog and gof  if : f(x) = c, c ∈ R, g(x) = sin `x^2`

Find fog and gof  if : f(x) = `x^2` + 2 , g (x) = 1 − `1/ (1-x)`.

Let f(x) = x² + x + 1 and g(x) = sin x. Show that fog ≠ gof.

If f(x) = |x|, prove that fof = f.

If f(x) = 2x + 5 and g(x) = x² + 1 be two real functions, then describe each of the following functions:
(1) fog
(2) gof
(3) fof
(4) f²
Also, show that fof ≠ f²

If f(x) = sin x and g(x) = 2x be two real functions, then describe gof and fog. Are these equal functions?

Let f, g, h be real functions given by f(x) = sin x, g (x) = 2x and h (x) = cos x. Prove that fog = go (fh).

Let  f  be any real function and let g be a function given by g(x) = 2x. Prove that gof = f + f.

   if `f (x) = sqrt(1-x)` and g(x) = `log_e` x are two real functions, then describe functions fog and gof.

  ` if  f : (-π/2 , π/2)` → R and g : [−1, 1]→ R be defined as f(x) = tan x and g(x) = `sqrt(1 - x^2)` respectively, describe fog and gof.

if f (x) = `sqrt (x +3) and  g (x) = x ^2 + 1` be two real functions, then find fog and gof.

Let f be a real function given by f (x)=`sqrt (x-2)`
Find each of the following:

(i) fof
(ii) fofof
(iii) (fofof) (38)
(iv) f²

Also, show that fof ≠ `f^2` .

Let

f (x) =`{ (1 + x, 0≤ x ≤ 2) , (3 -x , 2 < x ≤ 3):}`

Find fof.

 If f, g : R → R be two functions defined as f(x) = |x| + x and g(x) = |x|- x, ∀x∈R" .Then find fog and gof. Hence find fog(–3), fog(5) and gof (–2).

State with reason whether the following functions have inverse :
f : {1, 2, 3, 4} → {10} with f = {(1, 10), (2, 10), (3, 10), (4, 10)}

State with reason whether the following functions have inverse :

g : {5, 6, 7, 8} → {1, 2, 3, 4} with g = {(5, 4), (6, 3), (7, 4), (8, 2)}

State with reason whether the following functions have inverse:

h : {2, 3, 4, 5} → {7, 9, 11, 13} with h = {(2, 7), (3, 9), (4, 11), (5, 13)}

Find f ⁻¹ if it exists : f : A → B, where A = {0, −1, −3, 2}; B = {−9, −3, 0, 6} and f(x) = 3 x.

Find f ⁻¹ if it exists : f : A → B, where A = {1, 3, 5, 7, 9}; B = {0, 1, 9, 25, 49, 81} and f(x) = x²

Consider f : {1, 2, 3} → {a, b, c} and g : {a, b, c} → {apple, ball, cat} defined as f (1) = a, f (2) = b, f (3) = c, g (a) = apple, g (b) = ball and g (c) =  cat. Show that f, g and gof are invertible. Find f⁻¹, g⁻¹ and gof⁻¹and show that (gof)⁻¹ = f ⁻¹o g⁻¹

Let A = {1, 2, 3, 4}; B = {3, 5, 7, 9}; C = {7, 23, 47, 79} and f : A → B, g : B → C be defined as f(x) = 2x + 1 and g(x) = x² − 2. Express (gof)⁻¹ and f⁻¹ og⁻¹ as the sets of ordered pairs and verify that (gof)⁻¹ = f⁻¹ og⁻¹.

Show that the function f : Q → Q, defined by f(x) = 3x + 5, is invertible. Also, find f⁻¹

Consider f : R → R given by f(x) = 4x + 3. Show that f is invertible. Find the inverse of f.

Consider f : R → R₊ → [4, ∞) given by f(x) = x² + 4. Show that f is invertible with inverse f⁻¹ of f given by f⁻¹ `(x)= sqrt (x-4)` where R⁺ is the set of all non-negative real numbers.

if f(x) = `(4x + 3)/(6x - 4), x ≠  2/3` show that fof(x) = x, for all x ≠ 2/3 . What is the inverse of f?

Consider f : R₊ → [−5, ∞) given by f(x) = 9x² + 6x − 5. Show that f is invertible with `f^-1 (x) = (sqrt (x +6)-1)/3 .`

If f : R → R be defined by f(x) = x³ −3, then prove that f⁻¹ exists and find a formula for f⁻¹. Hence, find f⁻¹(24) and f⁻¹ (5).

A function f : R → R is defined as f(x) = x³ + 4. Is it a bijection or not? In case it is a bijection, find f⁻¹ (3).

If f : Q → Q, g : Q → Q are two functions defined by f(x) = 2 x and g(x) = x + 2, show that f and g are bijective maps. Verify that (gof)⁻¹ = f⁻¹ og ⁻¹.

Let A = R - {3} and B = R - {1}. Consider the function f : A → B defined by f(x) = `(x-2)/(x-3).`Show that f is one-one and onto and hence find f^-1.

                    [CBSE 2012, 2014]

Consider the function f : R⁺ →  [-9 , ∞ ]given by f(x) = 5x² + 6x - 9. Prove that f is invertible with f ^-1 (y) = `(sqrt(54 + 5y) -3)/5`             [CBSE 2015]

Let f : N→N be a function defined as f(x)=`9x^2`+6x−5. Show that f : N→S, where S is the range of f, is invertible. Find the inverse of f and hence find `f^-1`(43) and` f^−1`(163).

Let f : R `{- 4/3} `- 43 →">→ R be a function defined as f(x) = `(4x)/(3x +4)` . Show that f : R - `{-4/3}`→ Rang (f) is one-one and onto. Hence, find f ^-1.

If f : R → (−1, 1) defined by `f (x) = (10^x- 10^-x)/(10^x + 10 ^-x)` is invertible, find f⁻¹.

If f : R → (0, 2) defined by `f (x) =(e^x - e^(x))/(e^x +e^(-x))+1`is invertible , find f^-1.

Let f : [−1, ∞) → [−1, ∞) be given by f(x) = (x + 1)² − 1, x ≥ −1. Show that f is invertible. Also, find the set S = {x : f(x) = f⁻¹ (x)}.

Let A = {x &epsis; R | −1 ≤ x ≤ 1} and let f : A → A, g : A → A be two functions defined by f(x) = x² and g(x) = sin (π x/2). Show that g⁻¹ exists but f⁻¹ does not exist. Also, find g−1.

Let f be a function from R to R, such that f(x) = cos (x + 2). Is f invertible? Justify your answer.

If A = {1, 2, 3, 4} and B = {a, b, c, d}, define any four bijections from A to B. Also give their inverse functions.

Let A and B be two sets, each with a finite number of elements. Assume that there is an injective map from A to B and that there is an injective map from B to A. Prove that there is a bijection from A to B.

If f : A → A, g : A → A are two bijections, then prove that fog is an injection ?

If f : A → A, g : A → A are two bijections, then prove that fog is a surjection ?

Which one of the following graphs represents a function?

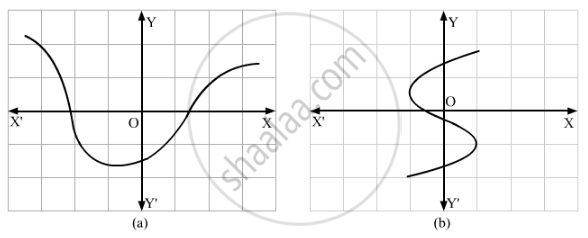
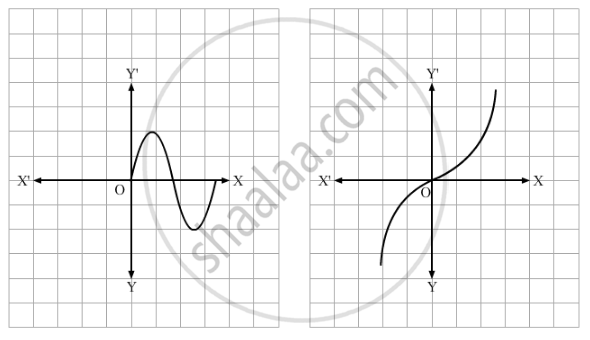
Which of the following graphs represents a one-one function?

If A = {1, 2, 3} and B = {a, b}, write the total number of functions from A to B.

If A = {a, b, c} and B = {−2, −1, 0, 1, 2}, write the total number of one-one functions from A to B.

Write the total number of one-one functions from set A = {1, 2, 3, 4} to set B = {a, b, c}.

If f : R → R is defined by f(x) = x², write f⁻¹ (25)

If f : C → C is defined by f(x) = x², write f⁻¹ (−4). Here, C denotes the set of all complex numbers.

If f : R → R is given by f(x) = x³, write f⁻¹ (1).

Let C denote the set of all complex numbers. A function f : C → C is defined by f(x) = x³. Write f⁻¹(1).

Let f  be a function from C (set of all complex numbers) to itself given by f(x) = x³. Write f⁻¹ (−1).

If f : C → C is defined by f(x) = x⁴, write f⁻¹ (1).

If f : R → R is defined by f(x) = x², find f⁻¹ (−25).

If f : C → C is defined by f(x) = (x − 2)³, write f⁻¹ (−1).

If f : R → R is defined by f(x) = 10 x − 7, then write f⁻¹ (x).

Let \[f : \left( - \frac{\pi}{2}, \frac{\pi}{2} \right) \to R\]  be a function defined by f(x) = cos [x]. Write range (f).

If f : R → R defined by f(x) = 3x − 4 is invertible, then write f⁻¹ (x).

If f : R → R, g : R → are given by f(x) = (x + 1)² and g(x) = x² + 1, then write the value of fog (−3).

Let A = {x ∈ R : −4 ≤ x ≤ 4 and x ≠ 0} and f : A → R be defined by \[f\left( x \right) = \frac{\left| x \right|}{x}\]Write the range of f.

Let \[f : \left[ - \frac{\pi}{2}, \frac{\pi}{2} \right] \to\] A be defined by f(x) = sin x. If f is a bijection, write set A.

Let f : R − {−1} → R − {1} be given by\[f\left( x \right) = \frac{x}{x + 1} . \text{Write } f^{- 1} \left( x \right)\]

Let `f : R - {- 3/5}` → R be a function defined as `f  (x) = (2x)/(5x +3).` 

f^-1 : Range of f → `R -{-3/5}`.

Let f : R → R, g : R → R be two functions defined by f(x) = x² + x + 1 and g(x) = 1 − x². Write fog (−2).

Let f : R → R be defined as  `f (x) = (2x - 3)/4.` write fo f^-1 (1) .

Let f be an invertible real function. Write ( f^-1  of ) (1) + ( f^-1  of ) (2) +..... +( f^-1 of ) (100 )

Let A = {1, 2, 3, 4} and B = {a, b} be two sets. Write the total number of onto functions from A to B.

Write the domain of the real function

`f (x) = sqrtx - [x] .`

Write the domain of the real function

`f (x) = sqrt([x] - x) .`

Write the domain of the real function

`f (x) = 1/(sqrt([x] - x)`.

Write whether f : R → R, given by `f(x) = x + sqrtx^2` is one-one, many-one, onto or into.

If f(x) = x + 7 and g(x) = x − 7, x ∈ R, write fog (7).

What is the range of the function

`f (x) = ([x - 1])/(x -1) ?`

If f : R → R be defined by f(x) = (3 − x³)1/3, then find fof (x).

If f : R → R is defined by f(x) = 3x + 2, find f (f (x)).

Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from A to B. State whether f is one-one or not.

If f : {5, 6} → {2, 3} and g : {2, 3} → {5, 6} are given by f = {(5, 2), (6, 3)} and g = {(2, 5), (3, 6)}, then find fog.    [NCERT EXEMPLAR]

Let f : R → R be the function defined by f(x) = 4x − 3 for all x ∈ R Then write f .   [NCERT EXEMPLAR]

Which one the following relations on A = {1, 2, 3} is a function?
f = {(1, 3), (2, 3), (3, 2)}, g = {(1, 2), (1, 3), (3, 1)}                                                                                                        [NCERT EXEMPLAR]

Write the domain of the real function f defined by f(x) = `sqrt (25 -x^2)`   [NCERT EXEMPLAR]

Let A = {a, b, c, d} and f : A → A be given by f = {( a,b ),( b , d ),( c , a ) , ( d , c )} write `f^-1`. [NCERT EXEMPLAR]

Let f, g : R → R be defined by f(x) = 2x + l and g(x) = x²−2 for all x

∈ R, respectively. Then, find gof.  [NCERT EXEMPLAR]

If the mapping f : {1, 3, 4} → {1, 2, 5} and g : {1, 2, 5} → {1, 3}, given by f = {(1, 2), (3, 5), (4, 1)} and g = {(2, 3), (5, 1), (1, 3)}, then write fog. [NCERT EXEMPLAR]

If a function g = {(1, 1), (2, 3), (3, 5), (4, 7)} is described by g(x) = \[\alpha x + \beta\]  then find the values of \[\alpha\] and \[ \beta\] . [NCERT EXEMPLAR]

If f(x) = 4 −( x - 7)3 then write f^-1 (x).

Let\[A = \left\{ x \in R : - 1 \leq x \leq 1 \right\} = \text{B and C} = \left\{ x \in R : x \geq 0 \right\} and\]\[S = \left\{ \left( x, y \right) \in A \times B : x^2 + y^2 = 1 \right\} \text{and } S_0 = \left\{ \left( x, y \right) \in A \times C : x^2 + y^2 = 1 \right\}\]

Then,

\[f : R \to R \text{given by} f\left( x \right) = x + \sqrt{x^2} \text{ is }\]

 \[f : A \to \text{B given by } 3^{ f\left( x \right)} + 2^{- x} = 4\] is a bijection, then

The function f : R → R defined by

`f (x) = 2^x + 2^(|x|)` is 

Let the function

\[f : R - \left\{ - b \right\} \to R - \left\{ 1 \right\}\]

\[f\left( x \right) = \frac{x + a}{x + b}, a \neq b .\text{Then},\]

The function 

f : A → B defined by 

f (x) = - x² + 6x - 8 is a bijection if 

Let 

\[A = \left\{ x \in R : - 1 \leq x \leq 1 \right\} = B\] Then, the mapping\[f : A \to \text{B given by} f\left( x \right) = x\left| x \right|\] is 

Let

f : R → R be given by

\[f\left( x \right) = \left[ x^2 \right] + \left[ x + 1 \right] - 3\]

where [x] denotes the greatest integer less than or equal to x. Then, f(x) is
 

(d) one-one and onto

Let M be the set of all 2 × 2 matrices with entries from the set R of real numbers. Then, the function f : M→ R defined by f(A) = |A| for every A ∈ M, is

The function \[f : [0, \infty ) \to \text {R given by } f\left( x \right) = \frac{x}{x + 1} is\]

The range of the function

\[f\left( x \right) =^{7 - x} P_{x - 3}\]

A function f  from the set of natural numbers to integers defined by

`{([n-1]/2," when  n is  odd"   is ),(-n/2,when  n  is  even ) :}`

Let f be an injective map with domain {x, y, z} and range {1, 2, 3}, such that exactly one of the following statements is correct and the remaining are false.

\[f\left( x \right) = 1, f\left( y \right) \neq 1, f\left( z \right) \neq 2 .\]

The value of

\[f^{- 1} \left( 1 \right)\] is 

Which of the following functions form Z to itself are bijections?

Which of the following functions from

to itself are bijections?

Let

\[A = \left\{ x : - 1 \leq x \leq 1 \right\} \text{and} f : A \to \text{A such that f}\left( x \right) = x|x|\]

If the function\[f : R \to \text{A given by} f\left( x \right) = \frac{x^2}{x^2 + 1}\] is a surjection, then A =

If a function\[f : [2, \infty )\text{ to B defined by f}\left( x \right) = x^2 - 4x + 5\] is a bijection, then B =

The function

\[f : R \to R\] defined by\[f\left( x \right) = \left( x - 1 \right) \left( x - 2 \right) \left( x - 3 \right)\]

(a) one-one but not onto
(b) onto but not one-one
(c) both one and onto
(d) neither one-one nor onto

The  function f : [-1/2, 1/2, 1/2] → [-π /2,π/2], defined by f (x) = `sin^-1` (3x - `4x^3`), is

Let

\[f : R \to R\]  be a function defined by

Let

\[f : R - \left\{ n \right\} \to R\]

Let

\[f : R \to R\] is defined by

\[f\left( x \right) = \frac{e^{x^2} - e^{- x^2}}{e^{x^2 + e^{- x^2}}} is\]

The function

A function f from the set of natural numbers to the set of integers defined by

\[f\left( n \right)\begin{cases}\frac{n - 1}{2}, & \text{when n is odd} \\ - \frac{n}{2}, & \text{when n is even}\end{cases}\]

Which of the following functions from

\[A = \left\{ x \in R : - 1 \leq x \leq 1 \right\}\]

\[f : Z \to Z\]  be given by

 ` f (x) = {(x/2, ", if  x is even" ) ,(0 , ", if  x  is  odd "):}`

Then,  f is

The function \[f : R \to R\] defined by

\[f\left( x \right) = 6^x + 6^{|x|}\] is 

Let  \[f\left( x \right) = x^2 and g\left( x \right) = 2^x\] Then, the solution set of the equation

If \[f : R \to R is given by f\left( x \right) = 3x - 5, then f^{- 1} \left( x \right)\] 

If \[g \left( f \left( x \right) \right) = \left| \sin x \right| \text{and} f \left( g \left( x \right) \right) = \left( \sin \sqrt{x} \right)^2 , \text{then}\]

The inverse of the function

\[f : R \to \left\{ x \in R : x < 1 \right\}\] given by

\[f\left( x \right) = \frac{e^x - e^{- x}}{e^x + e^{- x}}\] is 

Let

 \[A = \left\{ x \in R : x \geq 1 \right\}\] The inverse of the function, 

\[f : A \to A\] given by

\[f\left( x \right) = 2^{x \left( x - 1 \right)} , is\]

Let

\[A = \left\{ x \in R : x \leq 1 \right\} and f : A \to A\] be defined as

\[f\left( x \right) = x \left( 2 - x \right)\] Then,

\[f^{- 1} \left( x \right)\] is

Let  \[f\left( x \right) = \frac{1}{1 - x} . \text{Then}, \left\{ f o \left( fof \right) \right\} \left( x \right)\]

If the function

\[f : R \to R\]  be such that

\[f\left( x \right) = x - \left[ x \right]\] where [x] denotes the greatest integer less than or equal to x, then \[f^{- 1} \left( x \right)\]

If  \[F : [1, \infty ) \to [2, \infty )\] is given by

\[f\left( x \right) = x + \frac{1}{x}, then f^{- 1} \left( x \right)\]

Let  \[f\left( x \right) = \frac{\alpha x}{x + 1}, x \neq - 1\] Then, for what value of α is \[f \left( f\left( x \right) \right) = x?\]

The distinct linear functions that map [−1, 1] onto [0, 2] are

Let

\[f : [2, \infty ) \to X\] be defined by

\[f\left( x \right) = 4x - x^2\] Then, f is invertible if X =

If  \[f : R \to \left( - 1, 1 \right)\] is defined by

\[f\left( x \right) = \frac{- x|x|}{1 + x^2}, \text{ then } f^{- 1} \left( x \right)\] equals

Let [x] denote the greatest integer less than or equal to x. If \[f\left( x \right) = \sin^{- 1} x, g\left( x \right) = \left[ x^2 \right]\text{  and } h\left( x \right) = 2x, \frac{1}{2} \leq x \leq \frac{1}{\sqrt{2}}\]

If  \[g\left( x \right) = x^2 + x - 2\text{ and} \frac{1}{2} gof\left( x \right) = 2 x^2 - 5x + 2\] is equal to

If  \[f\left( x \right) = \sin^2 x\] and the composite function   \[g\left( f\left( x \right) \right) = \left| \sin x \right|\] then g(x) is equal to

If \[f : R \to R\] is given by \[f\left( x \right) = x^3 + 3, \text{then} f^{- 1} \left( x \right)\] is equal to

Let \[f\left(x\right) = x^3\] be a function with domain {0, 1, 2, 3}. Then domain of \[f^{-1}\] is ______.

Let 
\[f : R \to R\]  be given by \[f\left( x \right) = x^2 - 3\] Then, \[f^{- 1}\] is given by 

Mark the correct alternative in the following question:

Let f : R → R be given by f(x) = tanx. Then, f^-1(1) is

Mark the correct alternative in the following question:
Let f : R→ R be defined as, f(x) =  \[\begin{cases}2x, if x > 3 \\ x^2 , if 1 < x \leq 3 \\ 3x, if x \leq 1\end{cases}\] 

Then, find f( \[-\]1) + f(2) + f(4)

Mark the correct alternative in the following question:
Let A = {1, 2, ... , n} and B = {a, b}. Then the number of subjections from A into B is

Mark the correct alternative in the following question:

If the set A contains 5 elements and the set B contains 6 elements, then the number of one-one and onto mappings from A to B is

Mark the correct alternative in the following question:
If the set A contains 7 elements and the set B contains 10 elements, then the number one-one functions from A to B is

Mark the correct alternative in the following question:
Let f : R  \[-\] \[\left\{ \frac{3}{5} \right\}\] \[\to\]  R be defined by f(x) = \[\frac{3x + 2}{5x - 3}\] Then,