Advertisements
Advertisements
Question
Find f −1 if it exists : f : A → B, where A = {1, 3, 5, 7, 9}; B = {0, 1, 9, 25, 49, 81} and f(x) = x2
Solution
A = {1, 3, 5, 7, 9}; B = {0, 1, 9, 25, 49, 81} and f(x) = x2
Given: f(x) = x2
So, f = {(1, 1), (3, 9), (5, 25), (7,49), (9, 81)}
Clearly, f is one-one.
But this is not onto because the element 0 in the co-domain (B) has no pre-image in the domain (A) .
⇒ f is not a bijection.
So, f -1does not exist.
APPEARS IN
RELATED QUESTIONS
Check the injectivity and surjectivity of the following function:
f: Z → Z given by f(x) = x2
Check the injectivity and surjectivity of the following function:
f: R → R given by f(x) = x2
Find the number of all onto functions from the set {1, 2, 3, …, n} to itself.
Which of the following functions from A to B are one-one and onto?
f2 = {(2, a), (3, b), (4, c)} ; A = {2, 3, 4}, B = {a, b, c}
Let A = {−1, 0, 1} and f = {(x, x2) : x ∈ A}. Show that f : A → A is neither one-one nor onto.
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = sinx
Let A = {1, 2, 3}. Write all one-one from A to itself.
If A = {1, 2, 3}, show that a onto function f : A → A must be one-one.
Verify associativity for the following three mappings : f : N → Z0 (the set of non-zero integers), g : Z0 → Q and h : Q → R given by f(x) = 2x, g(x) = 1/x and h(x) = ex.
Find f −1 if it exists : f : A → B, where A = {0, −1, −3, 2}; B = {−9, −3, 0, 6} and f(x) = 3 x.
Show that the function f : Q → Q, defined by f(x) = 3x + 5, is invertible. Also, find f−1
Consider f : R+ → [−5, ∞) given by f(x) = 9x2 + 6x − 5. Show that f is invertible with `f^-1 (x) = (sqrt (x +6)-1)/3 .`
If f : R → R be defined by f(x) = x3 −3, then prove that f−1 exists and find a formula for f−1. Hence, find f−1(24) and f−1 (5).
A function f : R → R is defined as f(x) = x3 + 4. Is it a bijection or not? In case it is a bijection, find f−1 (3).
Consider the function f : R+ → [-9 , ∞ ]given by f(x) = 5x2 + 6x - 9. Prove that f is invertible with f -1 (y) = `(sqrt(54 + 5y) -3)/5` [CBSE 2015]
If f : R → (−1, 1) defined by `f (x) = (10^x- 10^-x)/(10^x + 10 ^-x)` is invertible, find f−1.
Let A and B be two sets, each with a finite number of elements. Assume that there is an injective map from A to B and that there is an injective map from B to A. Prove that there is a bijection from A to B.
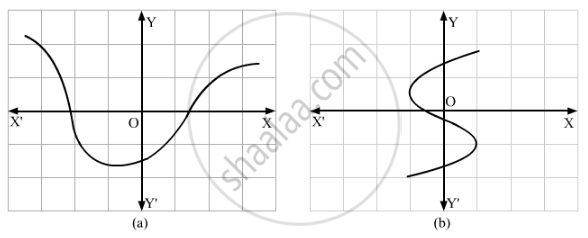
Which one of the following graphs represents a function?
Write the total number of one-one functions from set A = {1, 2, 3, 4} to set B = {a, b, c}.
If f : R → R is given by f(x) = x3, write f−1 (1).
If f : R → R defined by f(x) = 3x − 4 is invertible, then write f−1 (x).
\[f : A \to \text{B given by } 3^{ f\left( x \right)} + 2^{- x} = 4\] is a bijection, then
Which of the following functions from
to itself are bijections?
The function f : [-1/2, 1/2, 1/2] → [-π /2,π/2], defined by f (x) = `sin^-1` (3x - `4x^3`), is
The function
If \[f : R \to R is given by f\left( x \right) = 3x - 5, then f^{- 1} \left( x \right)\]
Let
\[A = \left\{ x \in R : x \geq 1 \right\}\] The inverse of the function,
\[f : A \to A\] given by
\[f\left( x \right) = 2^{x \left( x - 1 \right)} , is\]
If the function
\[f : R \to R\] be such that
\[f\left( x \right) = x - \left[ x \right]\] where [x] denotes the greatest integer less than or equal to x, then \[f^{- 1} \left( x \right)\]
Let A be a finite set. Then, each injective function from A into itself is not surjective.
Let f: R → R be the function defined by f(x) = 2x – 3 ∀ x ∈ R. write f–1
Are the following set of ordered pairs functions? If so, examine whether the mapping is injective or surjective.
{(a, b): a is a person, b is an ancestor of a}
Let A = [–1, 1]. Then, discuss whether the following functions defined on A are one-one, onto or bijective:
k(x) = x2
Using the definition, prove that the function f: A→ B is invertible if and only if f is both one-one and onto
Let f: R → R be the functions defined by f(x) = x3 + 5. Then f–1(x) is ______.
Given a function If as f(x) = 5x + 4, x ∈ R. If g : R → R is inverse of function ‘f then
`x^(log_5x) > 5` implies ______.
Let f: R→R be a polynomial function satisfying f(x + y) = f(x) + f(y) + 3xy(x + y) –1 ∀ x, y ∈ R and f'(0) = 1, then `lim_(x→∞)(f(2x))/(f(x)` is equal to ______.
Let S = {1, 2, 3, 4, 5, 6, 7}. Then the number of possible functions f: S `rightarrow` S such that f(m.n) = f(m).f(n) for every m, n ∈ S and m.n ∈ S is equal to ______.
Write the domain and range (principle value branch) of the following functions:
f(x) = tan–1 x.
