Advertisements
Advertisements
Question
Give an example of a function which is not one-one but onto ?
Solution
which is not one-one but onto
f: Z → N ∪ {0} given by f(x) = |x|
njectivity:
Let x and y be any two elements in the domain (Z), such that f(x) = f(y).
⇒ |x| = |y|
⇒ x= ± y
So, different elements of domain f may give the same image.
So, f is not one-one.
Surjectivity:
Let y be any element in the co domain (Z), such that f(x) = y for some element x in Z(domain).
f(x) = y
⇒ |x| = y
⇒ x = ± y
which is an element in Z (domain).
So, for every element in the co-domain, there exists a pre-image in the domain.
Thus, f is onto.
APPEARS IN
RELATED QUESTIONS
Following the case, state whether the function is one-one, onto, or bijective. Justify your answer.
f: R → R defined by f(x) = 1 + x2
Let f: R → R be defined as f(x) = 10x + 7. Find the function g: R → R such that g o f = f o g = 1R.
Classify the following function as injection, surjection or bijection : f : N → N given by f(x) = x3
Show that the function f : R − {3} → R − {2} given by f(x) = `(x-2)/(x-3)` is a bijection.
Let A = [-1, 1]. Then, discuss whether the following function from A to itself is one-one, onto or bijective : g(x) = |x|
If A = {1, 2, 3}, show that a one-one function f : A → A must be onto.
Let f : N → N be defined by
`f(n) = { (n+ 1, if n is odd),( n-1 , if n is even):}`
Show that f is a bijection.
[CBSE 2012, NCERT]
Let f = {(1, −1), (4, −2), (9, −3), (16, 4)} and g = {(−1, −2), (−2, −4), (−3, −6), (4, 8)}. Show that gof is defined while fog is not defined. Also, find gof.
Find fog (2) and gof (1) when : f : R → R ; f(x) = x2 + 8 and g : R → R; g(x) = 3x3 + 1.
Give examples of two functions f : N → N and g : N → N, such that gof is onto but f is not onto.
if `f (x) = sqrt(1-x)` and g(x) = `log_e` x are two real functions, then describe functions fog and gof.
Find f −1 if it exists : f : A → B, where A = {0, −1, −3, 2}; B = {−9, −3, 0, 6} and f(x) = 3 x.
Consider the function f : R+ → [-9 , ∞ ]given by f(x) = 5x2 + 6x - 9. Prove that f is invertible with f -1 (y) = `(sqrt(54 + 5y) -3)/5` [CBSE 2015]
If f : A → A, g : A → A are two bijections, then prove that fog is an injection ?
If f : R → R, g : R → are given by f(x) = (x + 1)2 and g(x) = x2 + 1, then write the value of fog (−3).
Let A = {x ∈ R : −4 ≤ x ≤ 4 and x ≠ 0} and f : A → R be defined by \[f\left( x \right) = \frac{\left| x \right|}{x}\]Write the range of f.
Let \[f : \left[ - \frac{\pi}{2}, \frac{\pi}{2} \right] \to\] A be defined by f(x) = sin x. If f is a bijection, write set A.
Let `f : R - {- 3/5}` → R be a function defined as `f (x) = (2x)/(5x +3).`
f-1 : Range of f → `R -{-3/5}`.
Let f be an invertible real function. Write ( f-1 of ) (1) + ( f-1 of ) (2) +..... +( f-1 of ) (100 )
Let f : R → R be the function defined by f(x) = 4x − 3 for all x ∈ R Then write f . [NCERT EXEMPLAR]
Let \[f\left( x \right) = \frac{\alpha x}{x + 1}, x \neq - 1\] Then, for what value of α is \[f \left( f\left( x \right) \right) = x?\]
Let
\[f : [2, \infty ) \to X\] be defined by
\[f\left( x \right) = 4x - x^2\] Then, f is invertible if X =
A function f: R→ R defined by f(x) = `(3x) /5 + 2`, x ∈ R. Show that f is one-one and onto. Hence find f−1.
If A = {a, b, c, d} and f = {a, b), (b, d), (c, a), (d, c)}, show that f is one-one from A onto A. Find f–1
Let f, g: R → R be two functions defined as f(x) = |x| + x and g(x) = x – x ∀ x ∈ R. Then, find f o g and g o f
Are the following set of ordered pairs functions? If so, examine whether the mapping is injective or surjective.
{(x, y): x is a person, y is the mother of x}
Which of the following functions from Z into Z are bijections?
Let g(x) = x2 – 4x – 5, then ____________.
Let A = R – {3}, B = R – {1}. Let f : A → B be defined by `"f"("x") = ("x" - 2)/("x" - 3)` Then, ____________.
The mapping f : N → N is given by f(n) = 1 + n2, n ∈ N when N is the set of natural numbers is ____________.
The function f: R → R defined as f(x) = x3 is:
Students of Grade 9, planned to plant saplings along straight lines, parallel to each other to one side of the playground ensuring that they had enough play area. Let us assume that they planted one of the rows of the saplings along the line y = x − 4. Let L be the set of all lines which are parallel on the ground and R be a relation on L.
Answer the following using the above information.
- Let f: R → R be defined by f(x) = x − 4. Then the range of f(x) is ____________.
Raji visited the Exhibition along with her family. The Exhibition had a huge swing, which attracted many children. Raji found that the swing traced the path of a Parabola as given by y = x2.
Answer the following questions using the above information.
- Let : N → R be defined by f(x) = x2. Range of the function among the following is ____________.
If f: R → R given by f(x) =(3 − x3)1/3, find f0f(x)
Consider a function f: `[0, pi/2] ->` R, given by f(x) = sinx and `g[0, pi/2] ->` R given by g(x) = cosx then f and g are
Let f: R→R be defined as f(x) = 2x – 1 and g: R – {1}→R be defined as g(x) = `(x - 1/2)/(x - 1)`. Then the composition function f (g(x)) is ______.
Consider a set containing function A= {cos–1cosx, sin(sin–1x), sinx((sinx)2 – 1), etan{x}, `e^(|cosx| + |sinx|)`, sin(tan(cosx)), sin(tanx)}. B, C, D, are subsets of A, such that B contains periodic functions, C contains even functions, D contains odd functions then the value of n(B ∩ C) + n(B ∩ D) is ______ where {.} denotes the fractional part of functions)
Let f(x) be a polynomial of degree 3 such that f(k) = `-2/k` for k = 2, 3, 4, 5. Then the value of 52 – 10f(10) is equal to ______.
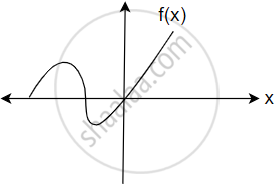
The given function f : R → R is not ‘onto’ function. Give reason.
