Advertisements
Advertisements
Question
If f : A → A, g : A → A are two bijections, then prove that fog is an injection ?
Solution
Injectivity of fog:
Let x and y be two elements of the domain (A), such that
(fog) (x) = (fog) (y)
⇒ f (g(x)) = f (g(y))
⇒ g (x) = g (y) (As, f is one-one)
⇒ x = y (As, g is one-one)
So, fog is an injection.
APPEARS IN
RELATED QUESTIONS
Let f: R → R be defined as f(x) = x4. Choose the correct answer.
Let f: R → R be defined as f(x) = 10x + 7. Find the function g: R → R such that g o f = f o g = 1R.
Find the number of all onto functions from the set {1, 2, 3, …, n} to itself.
Let A = {−1, 0, 1, 2}, B = {−4, −2, 0, 2} and f, g: A → B be functions defined by f(x) = x2 − x, x ∈ A and g(x) = `2|x - 1/2|- 1, x in A`. Are f and g equal?
Justify your answer. (Hint: One may note that two functions f: A → B and g: A → B such that f(a) = g(a) ∀ a ∈ A are called equal functions).
Classify the following function as injection, surjection or bijection :
f : Q → Q, defined by f(x) = x3 + 1
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = 3 − 4x
Find gof and fog when f : R → R and g : R → R is defined by f(x) = 2x + x2 and g(x) = x3
Find fog (2) and gof (1) when : f : R → R ; f(x) = x2 + 8 and g : R → R; g(x) = 3x3 + 1.
Consider f : N → N, g : N → N and h : N → R defined as f(x) = 2x, g(y) = 3y + 4 and h(z) = sin z for all x, y, z ∈ N. Show that ho (gof) = (hog) of.
Find fog and gof if : f (x) = ex g(x) = loge x .
Find fog and gof if : f (x) = x2 g(x) = cos x .
Let A = {1, 2, 3, 4}; B = {3, 5, 7, 9}; C = {7, 23, 47, 79} and f : A → B, g : B → C be defined as f(x) = 2x + 1 and g(x) = x2 − 2. Express (gof)−1 and f−1 og−1 as the sets of ordered pairs and verify that (gof)−1 = f−1 og−1.
If A = {1, 2, 3, 4} and B = {a, b, c, d}, define any four bijections from A to B. Also give their inverse functions.
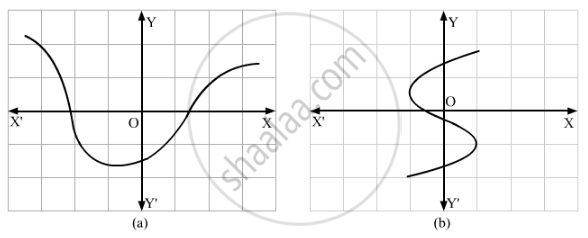
Which one of the following graphs represents a function?
If f : R → R is defined by f(x) = x2, write f−1 (25)
Let \[f : \left( - \frac{\pi}{2}, \frac{\pi}{2} \right) \to R\] be a function defined by f(x) = cos [x]. Write range (f).
Let f : R → R, g : R → R be two functions defined by f(x) = x2 + x + 1 and g(x) = 1 − x2. Write fog (−2).
Let A = {1, 2, 3, 4} and B = {a, b} be two sets. Write the total number of onto functions from A to B.
Write the domain of the real function
`f (x) = 1/(sqrt([x] - x)`.
The range of the function
\[f\left( x \right) =^{7 - x} P_{x - 3}\]
Which of the following functions from
to itself are bijections?
Let
\[A = \left\{ x : - 1 \leq x \leq 1 \right\} \text{and} f : A \to \text{A such that f}\left( x \right) = x|x|\]
If a function\[f : [2, \infty )\text{ to B defined by f}\left( x \right) = x^2 - 4x + 5\] is a bijection, then B =
Let
\[f : R \to R\] be a function defined by
Let
Let \[f\left( x \right) = \frac{\alpha x}{x + 1}, x \neq - 1\] Then, for what value of α is \[f \left( f\left( x \right) \right) = x?\]
If \[f : R \to R\] is given by \[f\left( x \right) = x^3 + 3, \text{then} f^{- 1} \left( x \right)\] is equal to
If f(x) = `(x+3)/(4x−5) , "g"(x) = (3+5x)/(4x−1)` then verify that `("fog") (x)` = x.
Let C be the set of complex numbers. Prove that the mapping f: C → R given by f(z) = |z|, ∀ z ∈ C, is neither one-one nor onto.
Let X = {1, 2, 3}and Y = {4, 5}. Find whether the following subset of X ×Y are function from X to Y or not
f = {(1, 4), (1, 5), (2, 4), (3, 5)}
Let f: R → R be given by f(x) = tan x. Then f–1(1) is ______.
Let f : R → R be a function defined by f(x) `= ("e"^abs"x" - "e"^-"x")/("e"^"x" + "e"^-"x")` then f(x) is
Let g(x) = x2 – 4x – 5, then ____________.
A function f: x → y is said to be one – one (or injective) if:
A function f: x → y is/are called onto (or surjective) if x under f.
Let n(A) = 4 and n(B) = 6, Then the number of one – one functions from 'A' to 'B' is:
The domain of the function `cos^-1((2sin^-1(1/(4x^2-1)))/π)` is ______.
Number of integral values of x satisfying the inequality `(3/4)^(6x + 10 - x^2) < 27/64` is ______.
Let A = R – {2} and B = R – {1}. If f: A `→` B is a function defined by f(x) = `(x - 1)/(x - 2)` then show that f is a one-one and an onto function.
