Advertisements
Advertisements
Question
if `f (x) = sqrt(1-x)` and g(x) = `log_e` x are two real functions, then describe functions fog and gof.
Solution
`f (x) = sqrt(1-x)`
For domain, 1-x≥0
⇒ x≤1
⇒ domain of f = (−∞, 1]
⇒ f : (−∞, 1] → (0,∞)
g(x) = loge x
Clearly, g : (0, ∞) → R
Computation of fog :
Clearly, the range of g is not a subset of the domain of f.
So,we need to compute the domain of fog.
⇒ Domain (fog) = {x : x ∈ Domain (g) and g(x) ∈ Domain of f}
⇒ Domain (fog) = {x: x ∈ (0, ∞) and loge x ∈ (−∞, 1]}
⇒ Domain (fog) = { x: x ∈ (0, ∞) and x ∈ (0, e] }
⇒ Domain (fog)= {x : x ∈ (0, e]}
⇒ Domain (fog )= (0, e]
⇒ fog : (0, e) → R
So, (fog) (x) = f (g (x))
= f (loge x)
= `sqrt( 1-log_e x)`
Computation of gof:Clearly, the range of f is a subset of the domain of g.
⇒ gof : (−∞,1] → R
⇒ (gof) (x) = g (f (x))
= `g (sqrt(1-x))`
= `log_e sqrt (1 - x)`
= `log_e (1 - x)^(1/2)`
= `1/2 log_e (1-x)`
APPEARS IN
RELATED QUESTIONS
Find the number of all onto functions from the set {1, 2, 3, …, n} to itself.
Give an example of a function which is neither one-one nor onto ?
Prove that the function f : N → N, defined by f(x) = x2 + x + 1, is one-one but not onto
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = 5x3 + 4
Suppose f1 and f2 are non-zero one-one functions from R to R. Is `f_1 / f^2` necessarily one - one? Justify your answer. Here,`f_1/f_2 : R → R is given by (f_1/f_2) (x) = (f_1(x))/(f_2 (x)) for all x in R .`
Find gof and fog when f : R → R and g : R → R is defined by f(x) = x2 + 8 and g(x) = 3x3 + 1 .
Let R+ be the set of all non-negative real numbers. If f : R+ → R+ and g : R+ → R+ are defined as `f(x)=x^2` and `g(x)=+sqrtx` , find fog and gof. Are they equal functions ?
Give examples of two functions f : N → N and g : N → N, such that gof is onto but f is not onto.
If f : A → B and g : B → C are one-one functions, show that gof is a one-one function.
If f(x) = sin x and g(x) = 2x be two real functions, then describe gof and fog. Are these equal functions?
Let f be a real function given by f (x)=`sqrt (x-2)`
Find each of the following:
(i) fof
(ii) fofof
(iii) (fofof) (38)
(iv) f2
Also, show that fof ≠ `f^2` .
Let
f (x) =`{ (1 + x, 0≤ x ≤ 2) , (3 -x , 2 < x ≤ 3):}`
Find fof.
State with reason whether the following functions have inverse:
h : {2, 3, 4, 5} → {7, 9, 11, 13} with h = {(2, 7), (3, 9), (4, 11), (5, 13)}
If A = {1, 2, 3, 4} and B = {a, b, c, d}, define any four bijections from A to B. Also give their inverse functions.
If f : A → A, g : A → A are two bijections, then prove that fog is a surjection ?
If f : R → R, g : R → are given by f(x) = (x + 1)2 and g(x) = x2 + 1, then write the value of fog (−3).
Write whether f : R → R, given by `f(x) = x + sqrtx^2` is one-one, many-one, onto or into.
If the mapping f : {1, 3, 4} → {1, 2, 5} and g : {1, 2, 5} → {1, 3}, given by f = {(1, 2), (3, 5), (4, 1)} and g = {(2, 3), (5, 1), (1, 3)}, then write fog. [NCERT EXEMPLAR]
Let\[A = \left\{ x \in R : - 1 \leq x \leq 1 \right\} = \text{B and C} = \left\{ x \in R : x \geq 0 \right\} and\]\[S = \left\{ \left( x, y \right) \in A \times B : x^2 + y^2 = 1 \right\} \text{and } S_0 = \left\{ \left( x, y \right) \in A \times C : x^2 + y^2 = 1 \right\}\]
Then,
\[f : R \to R \text{given by} f\left( x \right) = x + \sqrt{x^2} \text{ is }\]
Let \[f\left( x \right) = x^2 and g\left( x \right) = 2^x\] Then, the solution set of the equation
If \[f : R \to R is given by f\left( x \right) = 3x - 5, then f^{- 1} \left( x \right)\]
The inverse of the function
\[f : R \to \left\{ x \in R : x < 1 \right\}\] given by
\[f\left( x \right) = \frac{e^x - e^{- x}}{e^x + e^{- x}}\] is
Mark the correct alternative in the following question:
Let f : R → R be given by f(x) = tanx. Then, f-1(1) is
A function f: R→ R defined by f(x) = `(3x) /5 + 2`, x ∈ R. Show that f is one-one and onto. Hence find f−1.
Let f, g: R → R be two functions defined as f(x) = |x| + x and g(x) = x – x ∀ x ∈ R. Then, find f o g and g o f
Which of the following functions from Z into Z are bijections?
The mapping f : N → N is given by f(n) = 1 + n2, n ∈ N when N is the set of natural numbers is ____________.
The domain of the function `"f"("x") = 1/(sqrt ({"sin x"} + {"sin" ( pi + "x")}))` where {.} denotes fractional part, is
Students of Grade 9, planned to plant saplings along straight lines, parallel to each other to one side of the playground ensuring that they had enough play area. Let us assume that they planted one of the rows of the saplings along the line y = x − 4. Let L be the set of all lines which are parallel on the ground and R be a relation on L.
Answer the following using the above information.
- Let f: R → R be defined by f(x) = x − 4. Then the range of f(x) is ____________.
Let f: R → R defined by f(x) = 3x. Choose the correct answer
The solution set of the inequation log1/3(x2 + x + 1) + 1 > 0 is ______.
Let a and b are two positive integers such that b ≠ 1. Let g(a, b) = Number of lattice points inside the quadrilateral formed by lines x = 0, y = 0, x = b and y = a. f(a, b) = `[a/b] + [(2a)/b] + ... + [((b - 1)a)/b]`, then the value of `[(g(101, 37))/(f(101, 37))]` is ______.
(Note P(x, y) is lattice point if x, y ∈ I)
(where [.] denotes greatest integer function)
The graph of the function y = f(x) is symmetrical about the line x = 2, then ______.
For x ∈ R, x ≠ 0, let f0(x) = `1/(1 - x)` and fn+1 (x) = f0(fn(x)), n = 0, 1, 2, .... Then the value of `f_100(3) + f_1(2/3) + f_2(3/2)` is equal to ______.
A function f : [– 4, 4] `rightarrow` [0, 4] is given by f(x) = `sqrt(16 - x^2)`. Show that f is an onto function but not a one-one function. Further, find all possible values of 'a' for which f(a) = `sqrt(7)`.
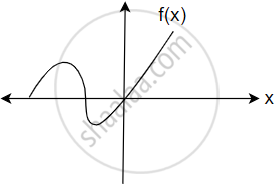
The given function f : R → R is not ‘onto’ function. Give reason.
