Advertisements
Advertisements
Question
The function
f : A → B defined by
f (x) = - x2 + 6x - 8 is a bijection if
Options
A = (- ∞ , 3] and B = ( - ∞, 1 ]
A = [- 3 , ∞) and B = ( - ∞, 1 ]
A = (- ∞ , 3] and B = [ 1 ,∞)
A = [3 ,∞ ) and B = [ 1 ,∞ )
Solution
\[A = ( - \infty , 3] \text{and }B = ( - \infty , 1]\]
\[f\left( x \right) = - x^2 + 6x - 8 , \text{is a polynomial function}\]
\[\text{And the domain of polynomial function is real number} . \]
\[ \therefore x \in R\]
\[f(x) = - x^2 + 6x - 8\]
\[ = - \left( x^2 - 6x + 8 \right)\]
\[ = - \left( x^2 - 6x + 9 - 1 \right)\]
\[ = - \left( x - 3 \right)^2 + 1\]
\[\text{Maximum value of} - \left( x - 3 \right)^2 \text{woud be } 0\]
\[ \therefore \text{Maximum value of} - \left( x - 3 \right)^2 + 1 \text{woud be} 1\]
\[ \therefore f(x) \in ( - \infty , 1]\]
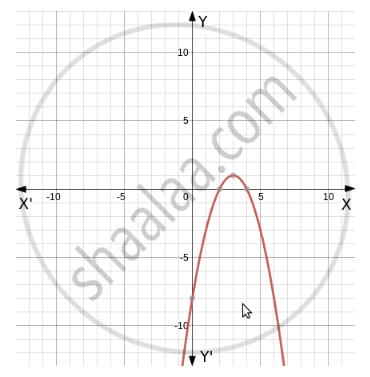
\[\text{We can see from the given graph that function is symmetrical about x = 3 & the given function is bijective .} \]
\[\text{So, x would be either} ( - \infty , 3 ] or [ 3, \infty )\]
\[\text{The correct option which satisfy A and B both is}: \]
\[A = ( - \infty , 3] \text{ and }B = ( - \infty , 1]\]
APPEARS IN
RELATED QUESTIONS
Let f: R → R be defined as f(x) = 3x. Choose the correct answer.
Let f: R → R be defined as f(x) = 10x + 7. Find the function g: R → R such that g o f = f o g = 1R.
Let S = {a, b, c} and T = {1, 2, 3}. Find F−1 of the following functions F from S to T, if it exists.
F = {(a, 3), (b, 2), (c, 1)}
Give an example of a function which is not one-one but onto ?
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = sinx
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = `x/(x^2 +1)`
Show that the function f : R − {3} → R − {2} given by f(x) = `(x-2)/(x-3)` is a bijection.
Show that the logarithmic function f : R0+ → R given by f (x) loga x ,a> 0 is a bijection.
Find gof and fog when f : R → R and g : R → R is defined by f(x) = x2 + 8 and g(x) = 3x3 + 1 .
Find gof and fog when f : R → R and g : R → R is defined by f(x) = x2 + 2x − 3 and g(x) = 3x − 4 .
Find fog and gof if : f (x) = x+1, g (x) = sin x .
If f(x) = 2x + 5 and g(x) = x2 + 1 be two real functions, then describe each of the following functions:
(1) fog
(2) gof
(3) fof
(4) f2
Also, show that fof ≠ f2
Let f, g, h be real functions given by f(x) = sin x, g (x) = 2x and h (x) = cos x. Prove that fog = go (fh).
Consider f : R → R+ → [4, ∞) given by f(x) = x2 + 4. Show that f is invertible with inverse f−1 of f given by f−1 `(x)= sqrt (x-4)` where R+ is the set of all non-negative real numbers.
What is the range of the function
`f (x) = ([x - 1])/(x -1) ?`
Let
f : R → R be given by
\[f\left( x \right) = \left[ x^2 \right] + \left[ x + 1 \right] - 3\]
where [x] denotes the greatest integer less than or equal to x. Then, f(x) is
(d) one-one and onto
Let f be an injective map with domain {x, y, z} and range {1, 2, 3}, such that exactly one of the following statements is correct and the remaining are false.
\[f\left( x \right) = 1, f\left( y \right) \neq 1, f\left( z \right) \neq 2 .\]
The value of
\[f^{- 1} \left( 1 \right)\] is
If \[g \left( f \left( x \right) \right) = \left| \sin x \right| \text{and} f \left( g \left( x \right) \right) = \left( \sin \sqrt{x} \right)^2 , \text{then}\]
Let
\[A = \left\{ x \in R : x \geq 1 \right\}\] The inverse of the function,
\[f : A \to A\] given by
\[f\left( x \right) = 2^{x \left( x - 1 \right)} , is\]
If \[g\left( x \right) = x^2 + x - 2\text{ and} \frac{1}{2} gof\left( x \right) = 2 x^2 - 5x + 2\] is equal to
Mark the correct alternative in the following question:
Let f : R \[-\] \[\left\{ \frac{3}{5} \right\}\] \[\to\] R be defined by f(x) = \[\frac{3x + 2}{5x - 3}\] Then,
Write about strlen() function.
Let the function f: R → R be defined by f(x) = 4x – 1, ∀ x ∈ R. Then, show that f is one-one.
Let R be the set of real numbers and f: R → R be the function defined by f(x) = 4x + 5. Show that f is invertible and find f–1.
Set A has 3 elements and the set B has 4 elements. Then the number of injective mappings that can be defined from A to B is ______.
The domain of the function f: R → R defined by f(x) = `sqrt(x^2 - 3x + 2)` is ______
Let the function f: R → R be defined by f(x) = cosx, ∀ x ∈ R. Show that f is neither one-one nor onto
Let X = {1, 2, 3}and Y = {4, 5}. Find whether the following subset of X ×Y are function from X to Y or not
k = {(1,4), (2, 5)}
Let f: R → R be defined by f(x) = `1/x` ∀ x ∈ R. Then f is ______.
Which of the following functions from Z into Z is bijective?
Let f : [0, ∞) → [0, 2] be defined by `"f" ("x") = (2"x")/(1 + "x"),` then f is ____________.
Let f : R `->` R be a function defined by f(x) = x3 + 4, then f is ______.
Raji visited the Exhibition along with her family. The Exhibition had a huge swing, which attracted many children. Raji found that the swing traced the path of a Parabola as given by y = x2.
Answer the following questions using the above information.
- The function f: Z → Z defined by f(x) = x2 is ____________.
Let f: R → R defined by f(x) = 3x. Choose the correct answer
Let x is a real number such that are functions involved are well defined then the value of `lim_(t→0)[max{(sin^-1 x/3 + cos^-1 x/3)^2, min(x^2 + 4x + 7)}]((sin^-1t)/t)` where [.] is greatest integer function and all other brackets are usual brackets.
Let f: R→R be a polynomial function satisfying f(x + y) = f(x) + f(y) + 3xy(x + y) –1 ∀ x, y ∈ R and f'(0) = 1, then `lim_(x→∞)(f(2x))/(f(x)` is equal to ______.
Let f(x) = ax (a > 0) be written as f(x) = f1(x) + f2(x), where f1(x) is an even function and f2(x) is an odd function. Then f1(x + y) + f1(x – y) equals ______.
