Advertisements
Advertisements
Question
What is the range of the function
`f (x) = ([x - 1])/(x -1) ?`
Solution
` f (x) = ([x - 1])/(x - 1) = (+(x-1)) /(x-1)` = ±1
Range of f = {-1 ,1 }
APPEARS IN
RELATED QUESTIONS
Check the injectivity and surjectivity of the following function:
f: N → N given by f(x) = x3
Give examples of two functions f: N → Z and g: Z → Z such that g o f is injective but gis not injective.
(Hint: Consider f(x) = x and g(x) =|x|)
Give an example of a function which is not one-one but onto ?
Classify the following function as injection, surjection or bijection :
f : Z → Z, defined by f(x) = x2 + x
Classify the following function as injection, surjection or bijection :
f : Z → Z, defined by f(x) = x − 5
Set of ordered pair of a function ? If so, examine whether the mapping is injective or surjective :{(a, b) : a is a person, b is an ancestor of a}
Find the number of all onto functions from the set A = {1, 2, 3, ..., n} to itself.
Suppose f1 and f2 are non-zero one-one functions from R to R. Is `f_1 / f^2` necessarily one - one? Justify your answer. Here,`f_1/f_2 : R → R is given by (f_1/f_2) (x) = (f_1(x))/(f_2 (x)) for all x in R .`
Find gof and fog when f : R → R and g : R → R is defined by f(x) = x and g(x) = |x| .
Let f : R → R and g : R → R be defined by f(x) = x + 1 and g (x) = x − 1. Show that fog = gof = IR.
Verify associativity for the following three mappings : f : N → Z0 (the set of non-zero integers), g : Z0 → Q and h : Q → R given by f(x) = 2x, g(x) = 1/x and h(x) = ex.
Find fog and gof if : f(x) = sin−1 x, g(x) = x2
Find fog and gof if : f(x) = `x^2` + 2 , g (x) = 1 − `1/ (1-x)`.
State with reason whether the following functions have inverse :
g : {5, 6, 7, 8} → {1, 2, 3, 4} with g = {(5, 4), (6, 3), (7, 4), (8, 2)}
Consider f : {1, 2, 3} → {a, b, c} and g : {a, b, c} → {apple, ball, cat} defined as f (1) = a, f (2) = b, f (3) = c, g (a) = apple, g (b) = ball and g (c) = cat. Show that f, g and gof are invertible. Find f−1, g−1 and gof−1and show that (gof)−1 = f −1o g−1
Consider f : R+ → [−5, ∞) given by f(x) = 9x2 + 6x − 5. Show that f is invertible with `f^-1 (x) = (sqrt (x +6)-1)/3 .`
Let A = R - {3} and B = R - {1}. Consider the function f : A → B defined by f(x) = `(x-2)/(x-3).`Show that f is one-one and onto and hence find f-1.
[CBSE 2012, 2014]
Let A and B be two sets, each with a finite number of elements. Assume that there is an injective map from A to B and that there is an injective map from B to A. Prove that there is a bijection from A to B.
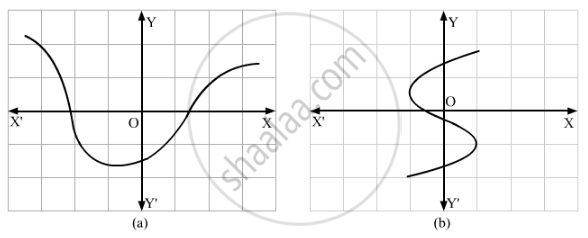
Which one of the following graphs represents a function?
Let C denote the set of all complex numbers. A function f : C → C is defined by f(x) = x3. Write f−1(1).
Let f : R → R, g : R → R be two functions defined by f(x) = x2 + x + 1 and g(x) = 1 − x2. Write fog (−2).
If f : R → R be defined by f(x) = (3 − x3)1/3, then find fof (x).
Let
\[A = \left\{ x \in R : x \leq 1 \right\} and f : A \to A\] be defined as
\[f\left( x \right) = x \left( 2 - x \right)\] Then,
\[f^{- 1} \left( x \right)\] is
Let [x] denote the greatest integer less than or equal to x. If \[f\left( x \right) = \sin^{- 1} x, g\left( x \right) = \left[ x^2 \right]\text{ and } h\left( x \right) = 2x, \frac{1}{2} \leq x \leq \frac{1}{\sqrt{2}}\]
Are the following set of ordered pairs functions? If so, examine whether the mapping is injective or surjective.
{(a, b): a is a person, b is an ancestor of a}
Let X = {1, 2, 3}and Y = {4, 5}. Find whether the following subset of X ×Y are function from X to Y or not
k = {(1,4), (2, 5)}
Let f: R → R be the functions defined by f(x) = x3 + 5. Then f–1(x) is ______.
Let f: R – `{3/5}` → R be defined by f(x) = `(3x + 2)/(5x - 3)`. Then ______.
Which of the following functions from Z into Z is bijective?
The function f : R → R given by f(x) = x3 – 1 is ____________.
Let f : R `->` R be a function defined by f(x) = x3 + 4, then f is ______.
A general election of Lok Sabha is a gigantic exercise. About 911 million people were eligible to vote and voter turnout was about 67%, the highest ever

Let I be the set of all citizens of India who were eligible to exercise their voting right in the general election held in 2019. A relation ‘R’ is defined on I as follows:
R = {(V1, V2) ∶ V1, V2 ∈ I and both use their voting right in the general election - 2019}
- Three friends F1, F2, and F3 exercised their voting right in general election-2019, then which of the following is true?
An organization conducted a bike race under 2 different categories-boys and girls. Totally there were 250 participants. Among all of them finally, three from Category 1 and two from Category 2 were selected for the final race. Ravi forms two sets B and G with these participants for his college project. Let B = {b1,b2,b3} G={g1,g2} where B represents the set of boys selected and G the set of girls who were selected for the final race.
Ravi decides to explore these sets for various types of relations and functions.
- Let R: B → G be defined by R = { (b1,g1), (b2,g2),(b3,g1)}, then R is ____________.
Let f: R → R defined by f(x) = x4. Choose the correct answer
The function f(x) = [x], where [x] denotes the greatest integer less than or equal to x; is continuous at ______.
