Advertisements
Advertisements
Question
Let f be a function from C (set of all complex numbers) to itself given by f(x) = x3. Write f−1 (−1).
Solution
\[Let f^{- 1} \left( - 1 \right) = x . . . \left( 1 \right)\]
\[ \Rightarrow f\left( x \right) = - 1\]
\[ \Rightarrow x^3 = - 1\]
\[ \Rightarrow x^3 + 1 = 0\]
\[ \Rightarrow \left( x + 1 \right)\left( x^2 - x + 1 \right) = 0 \left[ \text{using the identity}: a^3 + b^3 = \left( a + b \right)\left( a^2 - ab + b^2 \right) \right]\]
\[ \Rightarrow \left( x + 1 \right)\left( x + \omega \right)\left( x + \omega^2 \right) = 0, where \omega = \frac{1 \pm i\sqrt{3}}{2} \]
\[ \Rightarrow x = - 1, - \omega, - \omega^2 \left( asx \in C \right)\]
\[ \Rightarrow f^{- 1} \left( - 1 \right) = \left\{ - 1, - \omega, - \omega^2 \right\} [from\left( 1 \right)]\]
APPEARS IN
RELATED QUESTIONS
Let A = {−1, 0, 1, 2}, B = {−4, −2, 0, 2} and f, g: A → B be functions defined by f(x) = x2 − x, x ∈ A and g(x) = `2|x - 1/2|- 1, x in A`. Are f and g equal?
Justify your answer. (Hint: One may note that two functions f: A → B and g: A → B such that f(a) = g(a) ∀ a ∈ A are called equal functions).
If the function `f(x) = sqrt(2x - 3)` is invertible then find its inverse. Hence prove that `(fof^(-1))(x) = x`
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = x3 + 1
Show that the function f : R − {3} → R − {2} given by f(x) = `(x-2)/(x-3)` is a bijection.
If A = {1, 2, 3}, show that a onto function f : A → A must be one-one.
Show that if f1 and f2 are one-one maps from R to R, then the product f1 × f2 : R → R defined by (f1 × f2) (x) = f1 (x) f2 (x) need not be one - one.
Suppose f1 and f2 are non-zero one-one functions from R to R. Is `f_1 / f^2` necessarily one - one? Justify your answer. Here,`f_1/f_2 : R → R is given by (f_1/f_2) (x) = (f_1(x))/(f_2 (x)) for all x in R .`
Find gof and fog when f : R → R and g : R → R is defined by f(x) = 2x + x2 and g(x) = x3
Let f = {(1, −1), (4, −2), (9, −3), (16, 4)} and g = {(−1, −2), (−2, −4), (−3, −6), (4, 8)}. Show that gof is defined while fog is not defined. Also, find gof.
Let f : R → R and g : R → R be defined by f(x) = x + 1 and g (x) = x − 1. Show that fog = gof = IR.
Find fog and gof if : f (x) = x+1, g(x) = `e^x`
.
If f(x) = 2x + 5 and g(x) = x2 + 1 be two real functions, then describe each of the following functions:
(1) fog
(2) gof
(3) fof
(4) f2
Also, show that fof ≠ f2
If f(x) = sin x and g(x) = 2x be two real functions, then describe gof and fog. Are these equal functions?
Let
f (x) =`{ (1 + x, 0≤ x ≤ 2) , (3 -x , 2 < x ≤ 3):}`
Find fof.
Find f −1 if it exists : f : A → B, where A = {0, −1, −3, 2}; B = {−9, −3, 0, 6} and f(x) = 3 x.
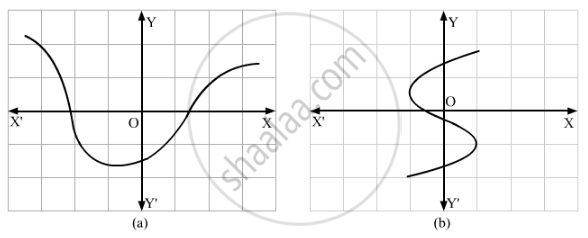
Which one of the following graphs represents a function?
Let C denote the set of all complex numbers. A function f : C → C is defined by f(x) = x3. Write f−1(1).
Let f be an invertible real function. Write ( f-1 of ) (1) + ( f-1 of ) (2) +..... +( f-1 of ) (100 )
Write the domain of the real function
`f (x) = 1/(sqrt([x] - x)`.
Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from A to B. State whether f is one-one or not.
Let f : R → R be the function defined by f(x) = 4x − 3 for all x ∈ R Then write f . [NCERT EXEMPLAR]
If the mapping f : {1, 3, 4} → {1, 2, 5} and g : {1, 2, 5} → {1, 3}, given by f = {(1, 2), (3, 5), (4, 1)} and g = {(2, 3), (5, 1), (1, 3)}, then write fog. [NCERT EXEMPLAR]
\[f : A \to \text{B given by } 3^{ f\left( x \right)} + 2^{- x} = 4\] is a bijection, then
The function \[f : [0, \infty ) \to \text {R given by } f\left( x \right) = \frac{x}{x + 1} is\]
Let
\[A = \left\{ x : - 1 \leq x \leq 1 \right\} \text{and} f : A \to \text{A such that f}\left( x \right) = x|x|\]
Let
\[f : Z \to Z\] be given by
` f (x) = {(x/2, ", if x is even" ) ,(0 , ", if x is odd "):}`
Then, f is
If f(x) = `(x+3)/(4x−5) , "g"(x) = (3+5x)/(4x−1)` then verify that `("fog") (x)` = x.
Write about strcmp() function.
Let f: R → R be given by f(x) = tan x. Then f–1(1) is ______.
The smallest integer function f(x) = [x] is ____________.
The function f : R → R defined by f(x) = 3 – 4x is ____________.
The function f : R → R given by f(x) = x3 – 1 is ____________.
Let f : R → R, g : R → R be two functions such that f(x) = 2x – 3, g(x) = x3 + 5. The function (fog)-1 (x) is equal to ____________.
Raji visited the Exhibition along with her family. The Exhibition had a huge swing, which attracted many children. Raji found that the swing traced the path of a Parabola as given by y = x2.
Answer the following questions using the above information.
- The function f: Z → Z defined by f(x) = x2 is ____________.
A function f: x → y is said to be one – one (or injective) if:
A function f: x → y is/are called onto (or surjective) if x under f.
Let the function f: R → R be defined by f(x) = 4x – 1, ∀ x ∈ R then 'f' is
If f; R → R f(x) = 10x + 3 then f–1(x) is:
