Advertisements
Advertisements
प्रश्न
Let f be a function from C (set of all complex numbers) to itself given by f(x) = x3. Write f−1 (−1).
उत्तर
\[Let f^{- 1} \left( - 1 \right) = x . . . \left( 1 \right)\]
\[ \Rightarrow f\left( x \right) = - 1\]
\[ \Rightarrow x^3 = - 1\]
\[ \Rightarrow x^3 + 1 = 0\]
\[ \Rightarrow \left( x + 1 \right)\left( x^2 - x + 1 \right) = 0 \left[ \text{using the identity}: a^3 + b^3 = \left( a + b \right)\left( a^2 - ab + b^2 \right) \right]\]
\[ \Rightarrow \left( x + 1 \right)\left( x + \omega \right)\left( x + \omega^2 \right) = 0, where \omega = \frac{1 \pm i\sqrt{3}}{2} \]
\[ \Rightarrow x = - 1, - \omega, - \omega^2 \left( asx \in C \right)\]
\[ \Rightarrow f^{- 1} \left( - 1 \right) = \left\{ - 1, - \omega, - \omega^2 \right\} [from\left( 1 \right)]\]
APPEARS IN
संबंधित प्रश्न
Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from A to B. Show that f is one-one.
Show that the function f: R → R given by f(x) = x3 is injective.
Given examples of two functions f: N → N and g: N → N such that gof is onto but f is not onto.
(Hint: Consider f(x) = x + 1 and `g(x) = {(x-1, ifx >1),(1, if x = 1):}`
Give an example of a function which is neither one-one nor onto ?
Classify the following function as injection, surjection or bijection : f : Z → Z given by f(x) = x3
Classify the following function as injection, surjection or bijection :
f : Z → Z, defined by f(x) = x2 + x
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = sinx
Classify the following function as injection, surjection or bijection :
f : Q → Q, defined by f(x) = x3 + 1
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = 5x3 + 4
Find gof and fog when f : R → R and g : R → R is defined by f(x) = 2x + 3 and g(x) = x2 + 5 .
Let f = {(1, −1), (4, −2), (9, −3), (16, 4)} and g = {(−1, −2), (−2, −4), (−3, −6), (4, 8)}. Show that gof is defined while fog is not defined. Also, find gof.
If f(x) = sin x and g(x) = 2x be two real functions, then describe gof and fog. Are these equal functions?
if `f (x) = sqrt(1-x)` and g(x) = `log_e` x are two real functions, then describe functions fog and gof.
` if f : (-π/2 , π/2)` → R and g : [−1, 1]→ R be defined as f(x) = tan x and g(x) = `sqrt(1 - x^2)` respectively, describe fog and gof.
Consider f : {1, 2, 3} → {a, b, c} and g : {a, b, c} → {apple, ball, cat} defined as f (1) = a, f (2) = b, f (3) = c, g (a) = apple, g (b) = ball and g (c) = cat. Show that f, g and gof are invertible. Find f−1, g−1 and gof−1and show that (gof)−1 = f −1o g−1
If f : R → (−1, 1) defined by `f (x) = (10^x- 10^-x)/(10^x + 10 ^-x)` is invertible, find f−1.
Write the total number of one-one functions from set A = {1, 2, 3, 4} to set B = {a, b, c}.
Write the domain of the real function
`f (x) = sqrt([x] - x) .`
Let\[A = \left\{ x \in R : - 1 \leq x \leq 1 \right\} = \text{B and C} = \left\{ x \in R : x \geq 0 \right\} and\]\[S = \left\{ \left( x, y \right) \in A \times B : x^2 + y^2 = 1 \right\} \text{and } S_0 = \left\{ \left( x, y \right) \in A \times C : x^2 + y^2 = 1 \right\}\]
Then,
Let f be an injective map with domain {x, y, z} and range {1, 2, 3}, such that exactly one of the following statements is correct and the remaining are false.
\[f\left( x \right) = 1, f\left( y \right) \neq 1, f\left( z \right) \neq 2 .\]
The value of
\[f^{- 1} \left( 1 \right)\] is
Let
\[f : R \to R\] be a function defined by
A function f from the set of natural numbers to the set of integers defined by
\[f\left( n \right)\begin{cases}\frac{n - 1}{2}, & \text{when n is odd} \\ - \frac{n}{2}, & \text{when n is even}\end{cases}\]
\[f : Z \to Z\] be given by
` f (x) = {(x/2, ", if x is even" ) ,(0 , ", if x is odd "):}`
Then, f is
Let \[f\left( x \right) = \frac{1}{1 - x} . \text{Then}, \left\{ f o \left( fof \right) \right\} \left( x \right)\]
If \[f : R \to \left( - 1, 1 \right)\] is defined by
\[f\left( x \right) = \frac{- x|x|}{1 + x^2}, \text{ then } f^{- 1} \left( x \right)\] equals
Mark the correct alternative in the following question:
Let f : R \[-\] \[\left\{ \frac{3}{5} \right\}\] \[\to\] R be defined by f(x) = \[\frac{3x + 2}{5x - 3}\] Then,
Let A = ℝ − {3}, B = ℝ − {1}. Let f : A → B be defined by \[f\left( x \right) = \frac{x - 2}{x - 3}, \forall x \in A\] Show that f is bijective. Also, find
(i) x, if f−1(x) = 4
(ii) f−1(7)
A function f: R→ R defined by f(x) = `(3x) /5 + 2`, x ∈ R. Show that f is one-one and onto. Hence find f−1.
Write about strcmp() function.
Set A has 3 elements and the set B has 4 elements. Then the number of injective mappings that can be defined from A to B is ______.
The smallest integer function f(x) = [x] is ____________.
The function f : R → R given by f(x) = x3 – 1 is ____________.
Raji visited the Exhibition along with her family. The Exhibition had a huge swing, which attracted many children. Raji found that the swing traced the path of a Parabola as given by y = x2.
Answer the following questions using the above information.
- Let f: {1,2,3,....} → {1,4,9,....} be defined by f(x) = x2 is ____________.
Let f: R → R defined by f(x) = 3x. Choose the correct answer
If log102 = 0.3010.log103 = 0.4771 then the number of ciphers after decimal before a significant figure comes in `(5/3)^-100` is ______.
The graph of the function y = f(x) is symmetrical about the line x = 2, then ______.
Let A = R – {2} and B = R – {1}. If f: A `→` B is a function defined by f(x) = `(x - 1)/(x - 2)` then show that f is a one-one and an onto function.
The trigonometric equation tan–1x = 3tan–1 a has solution for ______.
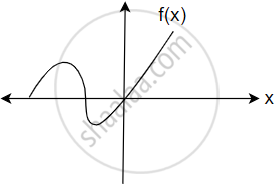
The given function f : R → R is not ‘onto’ function. Give reason.
