Advertisements
Advertisements
Question
Let
\[f : R - \left\{ n \right\} \to R\]
Options
f is one-one onto
f is one-one into
f is many one onto
f is many one into
Solution
Injectivity:
Let x and y be two elements in the domain R-{n}, such that
\[f\left( x \right) = f\left( y \right)\]
\[ \Rightarrow \frac{x - m}{x - n} = \frac{y - m}{y - n}\]
\[ \Rightarrow \left( x - m \right)\left( y - n \right) = \left( x - n \right)\left( y - m \right)\]
\[ \Rightarrow xy - nx - my + mn = xy - mx - ny + mn\]
\[ \Rightarrow \left( m - n \right)x = \left( m - n \right)y\]
\[ \Rightarrow x = y\]
So, f is one-one.
Surjectivity:
Let y be an element in the co domain R, such that
\[f\left( x \right) = y\]
\[ \Rightarrow \frac{x - m}{x - n} = y\]
\[ \Rightarrow x - m = xy - ny\]
\[ \Rightarrow ny - m = xy - x\]
\[ \Rightarrow ny - m = x\left( y - 1 \right)\]
\[ \Rightarrow x = \frac{ny - m}{y - 1}, \text{which is not defined for } y=1\]
\[So, 1 \in R\left( co domain \right)\text{has no pre image in }R-\left\{ n \right\}\]
\[\Rightarrow\] is not onto
Thus, the answer is (b) .
APPEARS IN
RELATED QUESTIONS
Following the case, state whether the function is one-one, onto, or bijective. Justify your answer.
f : R → R defined by f(x) = 3 − 4x
Let A and B be sets. Show that f: A × B → B × A such that (a, b) = (b, a) is bijective function.
Let f: R → R be defined as f(x) = 3x. Choose the correct answer.
If the function `f(x) = sqrt(2x - 3)` is invertible then find its inverse. Hence prove that `(fof^(-1))(x) = x`
Give an example of a function which is neither one-one nor onto ?
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = sinx
Classify the following function as injection, surjection or bijection :
f : Q → Q, defined by f(x) = x3 + 1
If f : R → R be the function defined by f(x) = 4x3 + 7, show that f is a bijection.
Find the number of all onto functions from the set A = {1, 2, 3, ..., n} to itself.
Given A = {2, 3, 4}, B = {2, 5, 6, 7}. Construct an example of each of the following:
(i) an injective map from A to B
(ii) a mapping from A to B which is not injective
(iii) a mapping from A to B.
Find gof and fog when f : R → R and g : R → R is defined by f(x) = x2 + 8 and g(x) = 3x3 + 1 .
Let f = {(3, 1), (9, 3), (12, 4)} and g = {(1, 3), (3, 3) (4, 9) (5, 9)}. Show that gof and fog are both defined. Also, find fog and gof.
Verify associativity for the following three mappings : f : N → Z0 (the set of non-zero integers), g : Z0 → Q and h : Q → R given by f(x) = 2x, g(x) = 1/x and h(x) = ex.
Let f(x) = x2 + x + 1 and g(x) = sin x. Show that fog ≠ gof.
If f(x) = sin x and g(x) = 2x be two real functions, then describe gof and fog. Are these equal functions?
A function f : R → R is defined as f(x) = x3 + 4. Is it a bijection or not? In case it is a bijection, find f−1 (3).
If A = {1, 2, 3, 4} and B = {a, b, c, d}, define any four bijections from A to B. Also give their inverse functions.
If f : C → C is defined by f(x) = x4, write f−1 (1).
Let f : R → R, g : R → R be two functions defined by f(x) = x2 + x + 1 and g(x) = 1 − x2. Write fog (−2).
Let\[A = \left\{ x \in R : - 1 \leq x \leq 1 \right\} = \text{B and C} = \left\{ x \in R : x \geq 0 \right\} and\]\[S = \left\{ \left( x, y \right) \in A \times B : x^2 + y^2 = 1 \right\} \text{and } S_0 = \left\{ \left( x, y \right) \in A \times C : x^2 + y^2 = 1 \right\}\]
Then,
The function
\[f : R \to R\] defined by\[f\left( x \right) = \left( x - 1 \right) \left( x - 2 \right) \left( x - 3 \right)\]
(a) one-one but not onto
(b) onto but not one-one
(c) both one and onto
(d) neither one-one nor onto
If the function
\[f : R \to R\] be such that
\[f\left( x \right) = x - \left[ x \right]\] where [x] denotes the greatest integer less than or equal to x, then \[f^{- 1} \left( x \right)\]
Mark the correct alternative in the following question:
Let f : R → R be given by f(x) = tanx. Then, f-1(1) is
Let A = ℝ − {3}, B = ℝ − {1}. Let f : A → B be defined by \[f\left( x \right) = \frac{x - 2}{x - 3}, \forall x \in A\] Show that f is bijective. Also, find
(i) x, if f−1(x) = 4
(ii) f−1(7)
A function f: R→ R defined by f(x) = `(3x) /5 + 2`, x ∈ R. Show that f is one-one and onto. Hence find f−1.
Let the function f: R → R be defined by f(x) = 4x – 1, ∀ x ∈ R. Then, show that f is one-one.
For sets A, B and C, let f: A → B, g: B → C be functions such that g o f is injective. Then both f and g are injective functions.
Let A = [–1, 1]. Then, discuss whether the following functions defined on A are one-one, onto or bijective:
f(x) = `x/2`
Let f: R → R be defined by f(x) = `1/x` ∀ x ∈ R. Then f is ______.
Raji visited the Exhibition along with her family. The Exhibition had a huge swing, which attracted many children. Raji found that the swing traced the path of a Parabola as given by y = x2.
Answer the following questions using the above information.
- Let : N → R be defined by f(x) = x2. Range of the function among the following is ____________.
If f: R → R given by f(x) =(3 − x3)1/3, find f0f(x)
A function f: x → y is/are called onto (or surjective) if x under f.
Consider a function f: `[0, pi/2] ->` R, given by f(x) = sinx and `g[0, pi/2] ->` R given by g(x) = cosx then f and g are
If f: R→R is a function defined by f(x) = `[x - 1]cos((2x - 1)/2)π`, where [ ] denotes the greatest integer function, then f is ______.
Number of integral values of x satisfying the inequality `(3/4)^(6x + 10 - x^2) < 27/64` is ______.
The graph of the function y = f(x) is symmetrical about the line x = 2, then ______.
If A = {x ∈ R: |x – 2| > 1}, B = `{x ∈ R : sqrt(x^2 - 3) > 1}`, C = {x ∈ R : |x – 4| ≥ 2} and Z is the set of all integers, then the number of subsets of the set (A ∩ B ∩ C) C ∩ Z is ______.
Which one of the following graphs is a function of x?
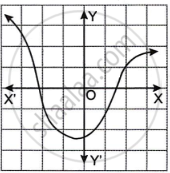 |
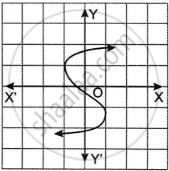 |
| Graph A | Graph B |
The trigonometric equation tan–1x = 3tan–1 a has solution for ______.
