Advertisements
Advertisements
Question
Give examples of two surjective functions f1 and f2 from Z to Z such that f1 + f2 is not surjective.
Solution
We know that f1: R → R, given by f1(x) = x, and f2(x) = -x are surjective functions.
Proving f1 is surjective :
Let y be an element in the co-domain (R), such that f1(x) = y.
f1(x) = y
⇒ x = y, which is in R.
So, for every element in the co-domain, there exists some pre-image in the domain.
So, f1is surjective .
Proving f2 is surjective :Let f2(x) = f2(y)−x =−yx = y
Let y be an element in the co domain (R) such that f2(x) = y.
f2(x) = y
⇒ x = y, which is in R.
So, for every element in the co-domain, there exists some pre-image in the domain.
So, f2 is surjective .
Proving (f1 + f2) is not surjective :
Given:
(f1 + f2) (x) = f1 (x) + f2 (x)= x + (-x) =0
So, for every real number x, (f1 + f2) (x)=0
So, the image of every number in the domain is same as 0.
⇒ Range = {0}
Co-domain = R
So, both are not same.
So, f1 + f2 is not surjective.
APPEARS IN
RELATED QUESTIONS
Check the injectivity and surjectivity of the following function:
f: R → R given by f(x) = x2
Let A = R − {3} and B = R − {1}. Consider the function f: A → B defined by `f(x) = ((x- 2)/(x -3))`. Is f one-one and onto? Justify your answer.
Let f: R → R be defined as f(x) = 10x + 7. Find the function g: R → R such that g o f = f o g = 1R.
Prove that the function f : N → N, defined by f(x) = x2 + x + 1, is one-one but not onto
Classify the following function as injection, surjection or bijection : f : N → N given by f(x) = x3
Classify the following function as injection, surjection or bijection :
f : Q → Q, defined by f(x) = x3 + 1
Let A = {1, 2, 3}. Write all one-one from A to itself.
Suppose f1 and f2 are non-zero one-one functions from R to R. Is `f_1 / f^2` necessarily one - one? Justify your answer. Here,`f_1/f_2 : R → R is given by (f_1/f_2) (x) = (f_1(x))/(f_2 (x)) for all x in R .`
Find gof and fog when f : R → R and g : R → R is defined by f(x) = x and g(x) = |x| .
Let A = {a, b, c}, B = {u v, w} and let f and g be two functions from A to B and from B to A, respectively, defined as :
f = {(a, v), (b, u), (c, w)}, g = {(u, b), (v, a), (w, c)}.
Show that f and g both are bijections and find fog and gof.
Find fog and gof if : f(x) = sin−1 x, g(x) = x2
if f (x) = `sqrt (x +3) and g (x) = x ^2 + 1` be two real functions, then find fog and gof.
If A = {1, 2, 3, 4} and B = {a, b, c, d}, define any four bijections from A to B. Also give their inverse functions.
Let A and B be two sets, each with a finite number of elements. Assume that there is an injective map from A to B and that there is an injective map from B to A. Prove that there is a bijection from A to B.
Which one of the following graphs represents a function?
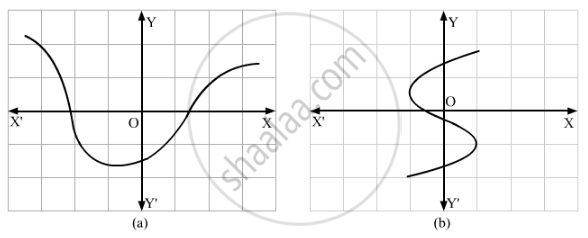
If f : R → R defined by f(x) = 3x − 4 is invertible, then write f−1 (x).
Let f : R → R+ be defined by f(x) = ax, a > 0 and a ≠ 1. Write f−1 (x).
Let `f : R - {- 3/5}` → R be a function defined as `f (x) = (2x)/(5x +3).`
f-1 : Range of f → `R -{-3/5}`.
Let f : R → R, g : R → R be two functions defined by f(x) = x2 + x + 1 and g(x) = 1 − x2. Write fog (−2).
Let f : R → R be defined as `f (x) = (2x - 3)/4.` write fo f-1 (1) .
If f(x) = x + 7 and g(x) = x − 7, x ∈ R, write fog (7).
If a function g = {(1, 1), (2, 3), (3, 5), (4, 7)} is described by g(x) = \[\alpha x + \beta\] then find the values of \[\alpha\] and \[ \beta\] . [NCERT EXEMPLAR]
The function \[f : [0, \infty ) \to \text {R given by } f\left( x \right) = \frac{x}{x + 1} is\]
Which of the following functions from
to itself are bijections?
If a function\[f : [2, \infty )\text{ to B defined by f}\left( x \right) = x^2 - 4x + 5\] is a bijection, then B =
Let
\[f : R \to R\] be given by \[f\left( x \right) = x^2 - 3\] Then, \[f^{- 1}\] is given by
If f(x) = `(x+3)/(4x−5) , "g"(x) = (3+5x)/(4x−1)` then verify that `("fog") (x)` = x.
Set A has 3 elements and the set B has 4 elements. Then the number of injective mappings that can be defined from A to B is ______.
Using the definition, prove that the function f: A→ B is invertible if and only if f is both one-one and onto
If f(x) = (4 – (x – 7)3}, then f–1(x) = ______.
The function f : A → B defined by f(x) = 4x + 7, x ∈ R is ____________.
The function f : R → R given by f(x) = x3 – 1 is ____________.
Sherlin and Danju are playing Ludo at home during Covid-19. While rolling the dice, Sherlin’s sister Raji observed and noted the possible outcomes of the throw every time belongs to set {1,2,3,4,5,6}. Let A be the set of players while B be the set of all possible outcomes.
A = {S, D}, B = {1,2,3,4,5,6}
- Raji wants to know the number of functions from A to B. How many number of functions are possible?
Students of Grade 9, planned to plant saplings along straight lines, parallel to each other to one side of the playground ensuring that they had enough play area. Let us assume that they planted one of the rows of the saplings along the line y = x − 4. Let L be the set of all lines which are parallel on the ground and R be a relation on L.
Answer the following using the above information.
- Let f: R → R be defined by f(x) = x − 4. Then the range of f(x) is ____________.
Let the function f: R → R be defined by f(x) = 4x – 1, ∀ x ∈ R then 'f' is
Function f: R → R, defined by f(x) = `x/(x^2 + 1)` ∀ x ∈ R is not
Consider a set containing function A= {cos–1cosx, sin(sin–1x), sinx((sinx)2 – 1), etan{x}, `e^(|cosx| + |sinx|)`, sin(tan(cosx)), sin(tanx)}. B, C, D, are subsets of A, such that B contains periodic functions, C contains even functions, D contains odd functions then the value of n(B ∩ C) + n(B ∩ D) is ______ where {.} denotes the fractional part of functions)
Let f(1, 3) `rightarrow` R be a function defined by f(x) = `(x[x])/(1 + x^2)`, where [x] denotes the greatest integer ≤ x, Then the range of f is ______.
Let f(x) be a polynomial of degree 3 such that f(k) = `-2/k` for k = 2, 3, 4, 5. Then the value of 52 – 10f(10) is equal to ______.
