Advertisements
Advertisements
Question
Find fog and gof if : f(x)= x + 1, g (x) = 2x + 3 .
Solution
f (x) = x+1, g (x) = 2x + 3
f : R→R ; g : R → R
Computing fog :
Clearly, the range of g is a subset of the domain of f.
⇒ fog : R→ R
(fog) (x) = f (g (x))
= f (2x+3)
= 2x + 3 + 1
= 2x + 4
Computing gof :
Clearly, the range of f is a subset of the domain of g.
⇒ fog : R → R
(gof) (x) = g (f (x))
= g (x+1)
= 2 ( x + 1) + 3
= 2x + 5
APPEARS IN
RELATED QUESTIONS
Check the injectivity and surjectivity of the following function:
f: N → N given by f(x) = x2
Check the injectivity and surjectivity of the following function:
f: N → N given by f(x) = x3
Let f: R → R be defined as f(x) = 3x. Choose the correct answer.
Let f: R → R be the Signum Function defined as
f(x) = `{(1,x>0), (0, x =0),(-1, x< 0):}`
and g: R → R be the Greatest Integer Function given by g(x) = [x], where [x] is greatest integer less than or equal to x. Then does fog and gof coincide in (0, 1]?
Which of the following functions from A to B are one-one and onto?
f1 = {(1, 3), (2, 5), (3, 7)} ; A = {1, 2, 3}, B = {3, 5, 7}
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = 5x3 + 4
Show that the exponential function f : R → R, given by f(x) = ex, is one-one but not onto. What happens if the co-domain is replaced by`R0^+` (set of all positive real numbers)?
If A = {1, 2, 3}, show that a one-one function f : A → A must be onto.
Find the number of all onto functions from the set A = {1, 2, 3, ..., n} to itself.
Give examples of two surjective functions f1 and f2 from Z to Z such that f1 + f2 is not surjective.
Find fog and gof if : f (x) = |x|, g (x) = sin x .
If f, g : R → R be two functions defined as f(x) = |x| + x and g(x) = |x|- x, ∀x∈R" .Then find fog and gof. Hence find fog(–3), fog(5) and gof (–2).
Find f −1 if it exists : f : A → B, where A = {1, 3, 5, 7, 9}; B = {0, 1, 9, 25, 49, 81} and f(x) = x2
Which of the following graphs represents a one-one function?
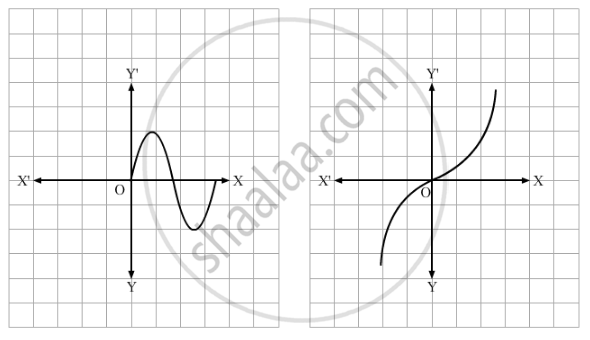
If A = {1, 2, 3} and B = {a, b}, write the total number of functions from A to B.
If A = {a, b, c} and B = {−2, −1, 0, 1, 2}, write the total number of one-one functions from A to B.
If f : R → R is defined by f(x) = x2, write f−1 (25)
Let C denote the set of all complex numbers. A function f : C → C is defined by f(x) = x3. Write f−1(1).
Let f be a function from C (set of all complex numbers) to itself given by f(x) = x3. Write f−1 (−1).
If f : R → R is defined by f(x) = x2, find f−1 (−25).
Let f : R − {−1} → R − {1} be given by\[f\left( x \right) = \frac{x}{x + 1} . \text{Write } f^{- 1} \left( x \right)\]
Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from A to B. State whether f is one-one or not.
Let\[A = \left\{ x \in R : - 1 \leq x \leq 1 \right\} = \text{B and C} = \left\{ x \in R : x \geq 0 \right\} and\]\[S = \left\{ \left( x, y \right) \in A \times B : x^2 + y^2 = 1 \right\} \text{and } S_0 = \left\{ \left( x, y \right) \in A \times C : x^2 + y^2 = 1 \right\}\]
Then,
Let
\[A = \left\{ x : - 1 \leq x \leq 1 \right\} \text{and} f : A \to \text{A such that f}\left( x \right) = x|x|\]
Let
Which of the following functions from
\[A = \left\{ x \in R : - 1 \leq x \leq 1 \right\}\]
If \[g\left( x \right) = x^2 + x - 2\text{ and} \frac{1}{2} gof\left( x \right) = 2 x^2 - 5x + 2\] is equal to
Mark the correct alternative in the following question:
Let f : R → R be given by f(x) = tanx. Then, f-1(1) is
Let f: R → R be the function defined by f(x) = 4x – 3 ∀ x ∈ R. Then write f–1
Show that the function f: R → R defined by f(x) = `x/(x^2 + 1)`, ∀ ∈ + R , is neither one-one nor onto
If f: R → R is defined by f(x) = x2 – 3x + 2, write f(f (x))
Let A = [–1, 1]. Then, discuss whether the following functions defined on A are one-one, onto or bijective:
f(x) = `x/2`
Let A = [–1, 1]. Then, discuss whether the following functions defined on A are one-one, onto or bijective:
h(x) = x|x|
Which of the following functions from Z into Z are bijections?
Sherlin and Danju are playing Ludo at home during Covid-19. While rolling the dice, Sherlin’s sister Raji observed and noted the possible outcomes of the throw every time belongs to set {1,2,3,4,5,6}. Let A be the set of players while B be the set of all possible outcomes.
A = {S, D}, B = {1,2,3,4,5,6}
- Raji wants to know the number of functions from A to B. How many number of functions are possible?
Raji visited the Exhibition along with her family. The Exhibition had a huge swing, which attracted many children. Raji found that the swing traced the path of a Parabola as given by y = x2.
Answer the following questions using the above information.
- Let : N → R be defined by f(x) = x2. Range of the function among the following is ____________.
If f: R→R is a function defined by f(x) = `[x - 1]cos((2x - 1)/2)π`, where [ ] denotes the greatest integer function, then f is ______.
Consider a set containing function A= {cos–1cosx, sin(sin–1x), sinx((sinx)2 – 1), etan{x}, `e^(|cosx| + |sinx|)`, sin(tan(cosx)), sin(tanx)}. B, C, D, are subsets of A, such that B contains periodic functions, C contains even functions, D contains odd functions then the value of n(B ∩ C) + n(B ∩ D) is ______ where {.} denotes the fractional part of functions)
Let f(x) = ax (a > 0) be written as f(x) = f1(x) + f2(x), where f1(x) is an even function and f2(x) is an odd function. Then f1(x + y) + f1(x – y) equals ______.
A function f : [– 4, 4] `rightarrow` [0, 4] is given by f(x) = `sqrt(16 - x^2)`. Show that f is an onto function but not a one-one function. Further, find all possible values of 'a' for which f(a) = `sqrt(7)`.
