Advertisements
Advertisements
प्रश्न
The function \[f : R \to R\] defined by
\[f\left( x \right) = 6^x + 6^{|x|}\] is
पर्याय
one-one and onto
many one and onto
one-one and into
many one and into
उत्तर
(d) many one and into
Graph of the given function is as follows :
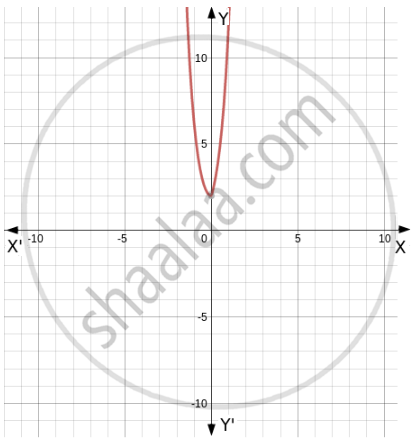
A line parallel to X axis is cutting the graph at two different values.
Therefore, for two different values of x we are getting the same value of y .
That means it is many one function .
From the given graph we can see that the range is
\[[2, \infty )\]b
and R is the codomain of the given function .
Hence, Codomain
\[\neq\] Range
Therefore, the given function is into .
APPEARS IN
संबंधित प्रश्न
Give examples of two functions f: N → Z and g: Z → Z such that g o f is injective but gis not injective.
(Hint: Consider f(x) = x and g(x) =|x|)
Given examples of two functions f: N → N and g: N → N such that gof is onto but f is not onto.
(Hint: Consider f(x) = x + 1 and `g(x) = {(x-1, ifx >1),(1, if x = 1):}`
Which of the following functions from A to B are one-one and onto?
f1 = {(1, 3), (2, 5), (3, 7)} ; A = {1, 2, 3}, B = {3, 5, 7}
Let A = {1, 2, 3}. Write all one-one from A to itself.
Find gof and fog when f : R → R and g : R → R is defined by f(x) = x2 + 8 and g(x) = 3x3 + 1 .
If f : A → B and g : B → C are onto functions, show that gof is a onto function.
Find fog and gof if : f (x) = x+1, g(x) = `e^x`
.
Find fog and gof if : f (x) = x+1, g (x) = sin x .
` if f : (-π/2 , π/2)` → R and g : [−1, 1]→ R be defined as f(x) = tan x and g(x) = `sqrt(1 - x^2)` respectively, describe fog and gof.
if f (x) = `sqrt (x +3) and g (x) = x ^2 + 1` be two real functions, then find fog and gof.
State with reason whether the following functions have inverse :
g : {5, 6, 7, 8} → {1, 2, 3, 4} with g = {(5, 4), (6, 3), (7, 4), (8, 2)}
If f : R → R be defined by f(x) = x3 −3, then prove that f−1 exists and find a formula for f−1. Hence, find f−1(24) and f−1 (5).
Consider the function f : R+ → [-9 , ∞ ]given by f(x) = 5x2 + 6x - 9. Prove that f is invertible with f -1 (y) = `(sqrt(54 + 5y) -3)/5` [CBSE 2015]
If f : R → (−1, 1) defined by `f (x) = (10^x- 10^-x)/(10^x + 10 ^-x)` is invertible, find f−1.
Let C denote the set of all complex numbers. A function f : C → C is defined by f(x) = x3. Write f−1(1).
Let f be a function from C (set of all complex numbers) to itself given by f(x) = x3. Write f−1 (−1).
Let \[f : \left[ - \frac{\pi}{2}, \frac{\pi}{2} \right] \to\] A be defined by f(x) = sin x. If f is a bijection, write set A.
If f : R → R be defined by f(x) = (3 − x3)1/3, then find fof (x).
Write the domain of the real function f defined by f(x) = `sqrt (25 -x^2)` [NCERT EXEMPLAR]
Let
\[A = \left\{ x \in R : - 1 \leq x \leq 1 \right\} = B\] Then, the mapping\[f : A \to \text{B given by} f\left( x \right) = x\left| x \right|\] is
Let
f : R → R be given by
\[f\left( x \right) = \left[ x^2 \right] + \left[ x + 1 \right] - 3\]
where [x] denotes the greatest integer less than or equal to x. Then, f(x) is
(d) one-one and onto
Let
\[f : R - \left\{ n \right\} \to R\]
\[f : R \to R\] is defined by
\[f\left( x \right) = \frac{e^{x^2} - e^{- x^2}}{e^{x^2 + e^{- x^2}}} is\]
Mark the correct alternative in the following question:
Let f : R → R be given by f(x) = tanx. Then, f-1(1) is
Mark the correct alternative in the following question:
Let f : R→ R be defined as, f(x) = \[\begin{cases}2x, if x > 3 \\ x^2 , if 1 < x \leq 3 \\ 3x, if x \leq 1\end{cases}\]
Then, find f( \[-\]1) + f(2) + f(4)
Are the following set of ordered pairs functions? If so, examine whether the mapping is injective or surjective.
{(x, y): x is a person, y is the mother of x}
Let the function f: R → R be defined by f(x) = cosx, ∀ x ∈ R. Show that f is neither one-one nor onto
Let A = R – {3}, B = R – {1}. Let f: A → B be defined by f(x) = `(x - 2)/(x - 3)` ∀ x ∈ A . Then show that f is bijective
If the set A contains 5 elements and the set B contains 6 elements, then the number of one-one and onto mappings from A to B is ______.
The mapping f : N → N is given by f(n) = 1 + n2, n ∈ N when N is the set of natural numbers is ____________.
Let f : [0, ∞) → [0, 2] be defined by `"f" ("x") = (2"x")/(1 + "x"),` then f is ____________.
If N be the set of all-natural numbers, consider f: N → N such that f(x) = 2x, ∀ x ∈ N, then f is ____________.
Range of `"f"("x") = sqrt((1 - "cos x") sqrt ((1 - "cos x")sqrt ((1 - "cos x")....infty))`
Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from A to B. Based on the given information, f is best defined as:
If f: R → R given by f(x) =(3 − x3)1/3, find f0f(x)
If f: R→R is a function defined by f(x) = `[x - 1]cos((2x - 1)/2)π`, where [ ] denotes the greatest integer function, then f is ______.
If f: [0, 1]→[0, 1] is defined by f(x) = `(x + 1)/4` and `d/(dx) underbrace(((fofof......of)(x)))_("n" "times")""|_(x = 1/2) = 1/"m"^"n"`, m ∈ N, then the value of 'm' is ______.
Let f(n) = `[1/3 + (3n)/100]n`, where [n] denotes the greatest integer less than or equal to n. Then `sum_(n = 1)^56f(n)` is equal to ______.
For x ∈ R, x ≠ 0, let f0(x) = `1/(1 - x)` and fn+1 (x) = f0(fn(x)), n = 0, 1, 2, .... Then the value of `f_100(3) + f_1(2/3) + f_2(3/2)` is equal to ______.
