Advertisements
Advertisements
प्रश्न
Which of the following functions from A to B are one-one and onto?
f1 = {(1, 3), (2, 5), (3, 7)} ; A = {1, 2, 3}, B = {3, 5, 7}
उत्तर
f1 = {(1, 3), (2, 5), (3, 7)} ; A = {1, 2, 3}, B = {3, 5, 7}
njectivity:
f1 (1) = 3
f1 (2) = 5
f1 (3) = 7
⇒ Every element of A has different images in B.
So, f1 is one-one.
Surjectivity:
Co-domain of f1 = {3, 5, 7}
Range of f1 =set of images = {3, 5, 7}
⇒ Co-domain = range
So, f1 is onto.
APPEARS IN
संबंधित प्रश्न
Let f: R → R be defined as f(x) = x4. Choose the correct answer.
Give an example of a function which is one-one but not onto ?
Classify the following function as injection, surjection or bijection : f : Z → Z given by f(x) = x3
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = x3 + 1
Let A = [-1, 1]. Then, discuss whether the following functions from A to itself is one-one, onto or bijective : h(x) = x2
Find fog (2) and gof (1) when : f : R → R ; f(x) = x2 + 8 and g : R → R; g(x) = 3x3 + 1.
Let f : R → R and g : R → R be defined by f(x) = x + 1 and g (x) = x − 1. Show that fog = gof = IR.
Find fog and gof if : f (x) = x+1, g (x) = sin x .
If f(x) = 2x + 5 and g(x) = x2 + 1 be two real functions, then describe each of the following functions:
(1) fog
(2) gof
(3) fof
(4) f2
Also, show that fof ≠ f2
Let f, g, h be real functions given by f(x) = sin x, g (x) = 2x and h (x) = cos x. Prove that fog = go (fh).
if `f (x) = sqrt(1-x)` and g(x) = `log_e` x are two real functions, then describe functions fog and gof.
` if f : (-π/2 , π/2)` → R and g : [−1, 1]→ R be defined as f(x) = tan x and g(x) = `sqrt(1 - x^2)` respectively, describe fog and gof.
Find f −1 if it exists : f : A → B, where A = {1, 3, 5, 7, 9}; B = {0, 1, 9, 25, 49, 81} and f(x) = x2
If f : R → R be defined by f(x) = x3 −3, then prove that f−1 exists and find a formula for f−1. Hence, find f−1(24) and f−1 (5).
If A = {1, 2, 3, 4} and B = {a, b, c, d}, define any four bijections from A to B. Also give their inverse functions.
If f : A → A, g : A → A are two bijections, then prove that fog is an injection ?
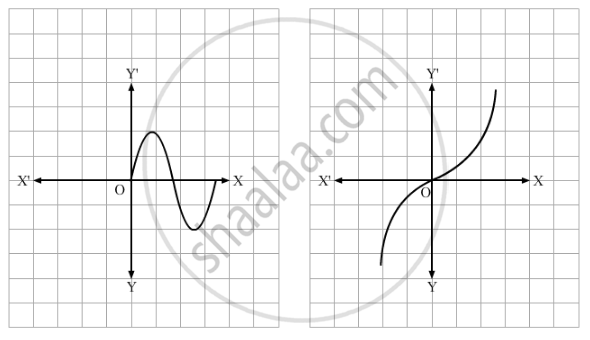
Which of the following graphs represents a one-one function?
If A = {a, b, c} and B = {−2, −1, 0, 1, 2}, write the total number of one-one functions from A to B.
Let `f : R - {- 3/5}` → R be a function defined as `f (x) = (2x)/(5x +3).`
f-1 : Range of f → `R -{-3/5}`.
Let A = {1, 2, 3, 4} and B = {a, b} be two sets. Write the total number of onto functions from A to B.
Write the domain of the real function
`f (x) = sqrt([x] - x) .`
Write the domain of the real function
`f (x) = 1/(sqrt([x] - x)`.
\[f : A \to \text{B given by } 3^{ f\left( x \right)} + 2^{- x} = 4\] is a bijection, then
The function f : R → R defined by
`f (x) = 2^x + 2^(|x|)` is
Let the function
\[f : R - \left\{ - b \right\} \to R - \left\{ 1 \right\}\]
\[f\left( x \right) = \frac{x + a}{x + b}, a \neq b .\text{Then},\]
If a function\[f : [2, \infty )\text{ to B defined by f}\left( x \right) = x^2 - 4x + 5\] is a bijection, then B =
If \[g \left( f \left( x \right) \right) = \left| \sin x \right| \text{and} f \left( g \left( x \right) \right) = \left( \sin \sqrt{x} \right)^2 , \text{then}\]
Write about strcmp() function.
The domain of the function f: R → R defined by f(x) = `sqrt(x^2 - 3x + 2)` is ______
Let D be the domain of the real valued function f defined by f(x) = `sqrt(25 - x^2)`. Then, write D
Let A = [–1, 1]. Then, discuss whether the following functions defined on A are one-one, onto or bijective:
h(x) = x|x|
Using the definition, prove that the function f: A→ B is invertible if and only if f is both one-one and onto
An organization conducted a bike race under 2 different categories-boys and girls. Totally there were 250 participants. Among all of them finally, three from Category 1 and two from Category 2 were selected for the final race. Ravi forms two sets B and G with these participants for his college project. Let B = {b1,b2,b3} G={g1,g2} where B represents the set of boys selected and G the set of girls who were selected for the final race.
Ravi decides to explore these sets for various types of relations and functions.
- Let R: B → G be defined by R = { (b1,g1), (b2,g2),(b3,g1)}, then R is ____________.
The solution set of the inequation log1/3(x2 + x + 1) + 1 > 0 is ______.
Let x is a real number such that are functions involved are well defined then the value of `lim_(t→0)[max{(sin^-1 x/3 + cos^-1 x/3)^2, min(x^2 + 4x + 7)}]((sin^-1t)/t)` where [.] is greatest integer function and all other brackets are usual brackets.
Let f(n) = `[1/3 + (3n)/100]n`, where [n] denotes the greatest integer less than or equal to n. Then `sum_(n = 1)^56f(n)` is equal to ______.
Let A = {1, 2, 3, ..., 10} and f : A `rightarrow` A be defined as
f(k) = `{{:(k + 1, if k "is odd"),( k, if k "is even"):}`.
Then the number of possible functions g : A `rightarrow` A such that gof = f is ______.
Let f(x) be a polynomial function of degree 6 such that `d/dx (f(x))` = (x – 1)3 (x – 3)2, then
Assertion (A): f(x) has a minimum at x = 1.
Reason (R): When `d/dx (f(x)) < 0, ∀ x ∈ (a - h, a)` and `d/dx (f(x)) > 0, ∀ x ∈ (a, a + h)`; where 'h' is an infinitesimally small positive quantity, then f(x) has a minimum at x = a, provided f(x) is continuous at x = a.
ASSERTION (A): The relation f : {1, 2, 3, 4} `rightarrow` {x, y, z, p} defined by f = {(1, x), (2, y), (3, z)} is a bijective function.
REASON (R): The function f : {1, 2, 3} `rightarrow` {x, y, z, p} such that f = {(1, x), (2, y), (3, z)} is one-one.
