Advertisements
Advertisements
प्रश्न
Let A = [-1, 1]. Then, discuss whether the following functions from A to itself is one-one, onto or bijective : h(x) = x2
उत्तर
h(x) = x2
Injection test:
Let x and y be any two elements in the domain (A), such that f(x) = f(y).
f(x) = f(y)
x2 = y2
x = ±y
So, f is not one-one.
Surjection test :
For y = - 1, there is no value of x in A.
So, f is not onto.
So, f is not bijective.
APPEARS IN
संबंधित प्रश्न
Let f: R → R be defined as f(x) = 3x. Choose the correct answer.
Show that the function f: R → R given by f(x) = x3 is injective.
Give examples of two functions f: N → Z and g: Z → Z such that g o f is injective but gis not injective.
(Hint: Consider f(x) = x and g(x) =|x|)
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = sin2x + cos2x
Show that the logarithmic function f : R0+ → R given by f (x) loga x ,a> 0 is a bijection.
Give examples of two surjective functions f1 and f2 from Z to Z such that f1 + f2 is not surjective.
Find fog (2) and gof (1) when : f : R → R ; f(x) = x2 + 8 and g : R → R; g(x) = 3x3 + 1.
Find fog and gof if : f (x) = x+1, g(x) = `e^x`
.
Let f be any real function and let g be a function given by g(x) = 2x. Prove that gof = f + f.
If f : C → C is defined by f(x) = x2, write f−1 (−4). Here, C denotes the set of all complex numbers.
If f : R → R is given by f(x) = x3, write f−1 (1).
Let f : R → R, g : R → R be two functions defined by f(x) = x2 + x + 1 and g(x) = 1 − x2. Write fog (−2).
If a function g = {(1, 1), (2, 3), (3, 5), (4, 7)} is described by g(x) = \[\alpha x + \beta\] then find the values of \[\alpha\] and \[ \beta\] . [NCERT EXEMPLAR]
\[f : A \to \text{B given by } 3^{ f\left( x \right)} + 2^{- x} = 4\] is a bijection, then
\[f : R \to R\] is defined by
\[f\left( x \right) = \frac{e^{x^2} - e^{- x^2}}{e^{x^2 + e^{- x^2}}} is\]
If \[g \left( f \left( x \right) \right) = \left| \sin x \right| \text{and} f \left( g \left( x \right) \right) = \left( \sin \sqrt{x} \right)^2 , \text{then}\]
If f(x) = `(x+3)/(4x−5) , "g"(x) = (3+5x)/(4x−1)` then verify that `("fog") (x)` = x.
If A = {a, b, c, d} and f = {a, b), (b, d), (c, a), (d, c)}, show that f is one-one from A onto A. Find f–1
Show that the function f: R → R defined by f(x) = `x/(x^2 + 1)`, ∀ ∈ + R , is neither one-one nor onto
Let R be the set of real numbers and f: R → R be the function defined by f(x) = 4x + 5. Show that f is invertible and find f–1.
Let A = [–1, 1]. Then, discuss whether the following functions defined on A are one-one, onto or bijective:
f(x) = `x/2`
Let A = [–1, 1]. Then, discuss whether the following functions defined on A are one-one, onto or bijective:
h(x) = x|x|
Let f: R → R be given by f(x) = tan x. Then f–1(1) is ______.
Let A = R – {3}, B = R – {1}. Let f : A → B be defined by `"f"("x") = ("x" - 2)/("x" - 3)` Then, ____________.
The function f : R → R given by f(x) = x3 – 1 is ____________.
Raji visited the Exhibition along with her family. The Exhibition had a huge swing, which attracted many children. Raji found that the swing traced the path of a Parabola as given by y = x2.
Answer the following questions using the above information.
- Let : N → R be defined by f(x) = x2. Range of the function among the following is ____________.
A function f: x → y is said to be one – one (or injective) if:
Let n(A) = 4 and n(B) = 6, Then the number of one – one functions from 'A' to 'B' is:
Prove that the function f is surjective, where f: N → N such that `f(n) = {{:((n + 1)/2",", if "n is odd"),(n/2",", if "n is even"):}` Is the function injective? Justify your answer.
Let [x] denote the greatest integer ≤ x, where x ∈ R. If the domain of the real valued function f(x) = `sqrt((|[x]| - 2)/(|[x]| - 3)` is (–∞, a) ∪ [b, c) ∪ [4, ∞), a < b < c, then the value of a + b + c is ______.
Number of integral values of x satisfying the inequality `(3/4)^(6x + 10 - x^2) < 27/64` is ______.
If A = {x ∈ R: |x – 2| > 1}, B = `{x ∈ R : sqrt(x^2 - 3) > 1}`, C = {x ∈ R : |x – 4| ≥ 2} and Z is the set of all integers, then the number of subsets of the set (A ∩ B ∩ C) C ∩ Z is ______.
A function f : [– 4, 4] `rightarrow` [0, 4] is given by f(x) = `sqrt(16 - x^2)`. Show that f is an onto function but not a one-one function. Further, find all possible values of 'a' for which f(a) = `sqrt(7)`.
Let f(x) be a polynomial function of degree 6 such that `d/dx (f(x))` = (x – 1)3 (x – 3)2, then
Assertion (A): f(x) has a minimum at x = 1.
Reason (R): When `d/dx (f(x)) < 0, ∀ x ∈ (a - h, a)` and `d/dx (f(x)) > 0, ∀ x ∈ (a, a + h)`; where 'h' is an infinitesimally small positive quantity, then f(x) has a minimum at x = a, provided f(x) is continuous at x = a.
ASSERTION (A): The relation f : {1, 2, 3, 4} `rightarrow` {x, y, z, p} defined by f = {(1, x), (2, y), (3, z)} is a bijective function.
REASON (R): The function f : {1, 2, 3} `rightarrow` {x, y, z, p} such that f = {(1, x), (2, y), (3, z)} is one-one.
Find the domain of sin–1 (x2 – 4).
Which one of the following graphs is a function of x?
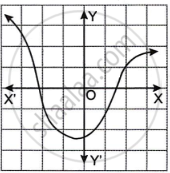 |
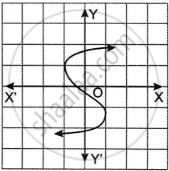 |
| Graph A | Graph B |
