Advertisements
Advertisements
प्रश्न
Let A = [–1, 1]. Then, discuss whether the following functions defined on A are one-one, onto or bijective:
h(x) = x|x|
उत्तर
Given, A = [–1, 1]
Let h(x1) = h(x2)
x1|x1| = x2|x2|
If x1, x2 > 0
x12 = x22
x12 – x22 = 0
(x1 – x2)(x1 + x2) = 0
x1 = x2 (as x1 + x2 ≠ 0)
Similarly for x1, x2 < 0, we have x1 = x2
It’s clearly seen that for x1 and x2 of opposite sign, x1 ≠ x2.
Hence, f(x) is one-one.
For x ∈ [0, 1], f(x) = x2 ∈ [0, 1]
For x < 0, f(x) = – x2 ∈ [–1, 0)
Hence, the range is [–1, 1].
So, h(x) is onto.
Therefore, h(x) is bijective.
APPEARS IN
संबंधित प्रश्न
Classify the following function as injection, surjection or bijection :
f : Q − {3} → Q, defined by `f (x) = (2x +3)/(x-3)`
Set of ordered pair of a function ? If so, examine whether the mapping is injective or surjective :{(a, b) : a is a person, b is an ancestor of a}
If A = {1, 2, 3}, show that a one-one function f : A → A must be onto.
Given A = {2, 3, 4}, B = {2, 5, 6, 7}. Construct an example of each of the following:
(i) an injective map from A to B
(ii) a mapping from A to B which is not injective
(iii) a mapping from A to B.
Let f be a real function given by f (x)=`sqrt (x-2)`
Find each of the following:
(i) fof
(ii) fofof
(iii) (fofof) (38)
(iv) f2
Also, show that fof ≠ `f^2` .
Let \[f : \left( - \frac{\pi}{2}, \frac{\pi}{2} \right) \to R\] be a function defined by f(x) = cos [x]. Write range (f).
Let
\[A = \left\{ x : - 1 \leq x \leq 1 \right\} \text{and} f : A \to \text{A such that f}\left( x \right) = x|x|\]
The function
\[f : R \to R\] defined by\[f\left( x \right) = \left( x - 1 \right) \left( x - 2 \right) \left( x - 3 \right)\]
(a) one-one but not onto
(b) onto but not one-one
(c) both one and onto
(d) neither one-one nor onto
Let
\[f : R - \left\{ n \right\} \to R\]
If \[F : [1, \infty ) \to [2, \infty )\] is given by
\[f\left( x \right) = x + \frac{1}{x}, then f^{- 1} \left( x \right)\]
If \[g\left( x \right) = x^2 + x - 2\text{ and} \frac{1}{2} gof\left( x \right) = 2 x^2 - 5x + 2\] is equal to
Let X = {1, 2, 3}and Y = {4, 5}. Find whether the following subset of X ×Y are function from X to Y or not
f = {(1, 4), (1, 5), (2, 4), (3, 5)}
Let A = R – {3}, B = R – {1}. Let f: A → B be defined by f(x) = `(x - 2)/(x - 3)` ∀ x ∈ A . Then show that f is bijective
Let f : R → R be defind by f(x) = `1/"x" AA "x" in "R".` Then f is ____________.
Let X = {-1, 0, 1}, Y = {0, 2} and a function f : X → Y defiend by y = 2x4, is ____________.
Let A = R – {3}, B = R – {1}. Let f : A → B be defined by `"f"("x") = ("x" - 2)/("x" - 3)` Then, ____________.
An organization conducted a bike race under 2 different categories-boys and girls. Totally there were 250 participants. Among all of them finally, three from Category 1 and two from Category 2 were selected for the final race. Ravi forms two sets B and G with these participants for his college project. Let B = {b1,b2,b3} G={g1,g2} where B represents the set of boys selected and G the set of girls who were selected for the final race.
Ravi decides to explore these sets for various types of relations and functions.
- Ravi wants to know among those relations, how many functions can be formed from B to G?
An organization conducted a bike race under 2 different categories-boys and girls. Totally there were 250 participants. Among all of them finally, three from Category 1 and two from Category 2 were selected for the final race. Ravi forms two sets B and G with these participants for his college project. Let B = {b1,b2,b3} G={g1,g2} where B represents the set of boys selected and G the set of girls who were selected for the final race.
Ravi decides to explore these sets for various types of relations and functions.
- Let R: B → G be defined by R = { (b1,g1), (b2,g2),(b3,g1)}, then R is ____________.
Raji visited the Exhibition along with her family. The Exhibition had a huge swing, which attracted many children. Raji found that the swing traced the path of a Parabola as given by y = x2.
Answer the following questions using the above information.
- The function f: Z → Z defined by f(x) = x2 is ____________.
Let n(A) = 4 and n(B) = 6, Then the number of one – one functions from 'A' to 'B' is:
Let the function f: R → R be defined by f(x) = 4x – 1, ∀ x ∈ R then 'f' is
Function f: R → R, defined by f(x) = `x/(x^2 + 1)` ∀ x ∈ R is not
Consider a set containing function A= {cos–1cosx, sin(sin–1x), sinx((sinx)2 – 1), etan{x}, `e^(|cosx| + |sinx|)`, sin(tan(cosx)), sin(tanx)}. B, C, D, are subsets of A, such that B contains periodic functions, C contains even functions, D contains odd functions then the value of n(B ∩ C) + n(B ∩ D) is ______ where {.} denotes the fractional part of functions)
Let f: R→R be a polynomial function satisfying f(x + y) = f(x) + f(y) + 3xy(x + y) –1 ∀ x, y ∈ R and f'(0) = 1, then `lim_(x→∞)(f(2x))/(f(x)` is equal to ______.
Let a and b are two positive integers such that b ≠ 1. Let g(a, b) = Number of lattice points inside the quadrilateral formed by lines x = 0, y = 0, x = b and y = a. f(a, b) = `[a/b] + [(2a)/b] + ... + [((b - 1)a)/b]`, then the value of `[(g(101, 37))/(f(101, 37))]` is ______.
(Note P(x, y) is lattice point if x, y ∈ I)
(where [.] denotes greatest integer function)
The graph of the function y = f(x) is symmetrical about the line x = 2, then ______.
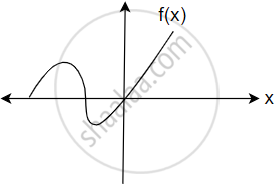
The given function f : R → R is not ‘onto’ function. Give reason.
