Advertisements
Advertisements
प्रश्न
Find the number of all onto functions from the set A = {1, 2, 3, ..., n} to itself.
उत्तर
We know that every onto function from A to itself is one-one.
So, the number of one-one functions = number of bijections = n!
APPEARS IN
संबंधित प्रश्न
Check the injectivity and surjectivity of the following function:
f: Z → Z given by f(x) = x2
Check the injectivity and surjectivity of the following function:
f: R → R given by f(x) = x2
Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from A to B. Show that f is one-one.
Let f: R → R be defined as f(x) = x4. Choose the correct answer.
Find the number of all onto functions from the set {1, 2, 3, …, n} to itself.
Give an example of a function which is neither one-one nor onto ?
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = sin2x + cos2x
Find fog and gof if : f(x) = `x^2` + 2 , g (x) = 1 − `1/ (1-x)`.
Let f(x) = x2 + x + 1 and g(x) = sin x. Show that fog ≠ gof.
If f(x) = 2x + 5 and g(x) = x2 + 1 be two real functions, then describe each of the following functions:
(1) fog
(2) gof
(3) fof
(4) f2
Also, show that fof ≠ f2
Let f : [−1, ∞) → [−1, ∞) be given by f(x) = (x + 1)2 − 1, x ≥ −1. Show that f is invertible. Also, find the set S = {x : f(x) = f−1 (x)}.
If A = {1, 2, 3, 4} and B = {a, b, c, d}, define any four bijections from A to B. Also give their inverse functions.
If A = {1, 2, 3} and B = {a, b}, write the total number of functions from A to B.
If f : C → C is defined by f(x) = x2, write f−1 (−4). Here, C denotes the set of all complex numbers.
If f : C → C is defined by f(x) = x4, write f−1 (1).
Let \[f : \left[ - \frac{\pi}{2}, \frac{\pi}{2} \right] \to\] A be defined by f(x) = sin x. If f is a bijection, write set A.
What is the range of the function
`f (x) = ([x - 1])/(x -1) ?`
If f : R → R be defined by f(x) = (3 − x3)1/3, then find fof (x).
Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from A to B. State whether f is one-one or not.
Let\[A = \left\{ x \in R : - 1 \leq x \leq 1 \right\} = \text{B and C} = \left\{ x \in R : x \geq 0 \right\} and\]\[S = \left\{ \left( x, y \right) \in A \times B : x^2 + y^2 = 1 \right\} \text{and } S_0 = \left\{ \left( x, y \right) \in A \times C : x^2 + y^2 = 1 \right\}\]
Then,
Let
\[A = \left\{ x \in R : - 1 \leq x \leq 1 \right\} = B\] Then, the mapping\[f : A \to \text{B given by} f\left( x \right) = x\left| x \right|\] is
A function f from the set of natural numbers to integers defined by
`{([n-1]/2," when n is odd" is ),(-n/2,when n is even ) :}`
Let \[f\left( x \right) = x^2 and g\left( x \right) = 2^x\] Then, the solution set of the equation
If \[f : R \to R is given by f\left( x \right) = 3x - 5, then f^{- 1} \left( x \right)\]
If \[f : R \to \left( - 1, 1 \right)\] is defined by
\[f\left( x \right) = \frac{- x|x|}{1 + x^2}, \text{ then } f^{- 1} \left( x \right)\] equals
Let \[f\left(x\right) = x^3\] be a function with domain {0, 1, 2, 3}. Then domain of \[f^{-1}\] is ______.
Mark the correct alternative in the following question:
Let f : R→ R be defined as, f(x) = \[\begin{cases}2x, if x > 3 \\ x^2 , if 1 < x \leq 3 \\ 3x, if x \leq 1\end{cases}\]
Then, find f( \[-\]1) + f(2) + f(4)
For sets A, B and C, let f: A → B, g: B → C be functions such that g o f is surjective. Then g is surjective.
Let A = {1, 2, 3, ...n} and B = {a, b}. Then the number of surjections from A into B is ______.
Let f: R – `{3/5}` → R be defined by f(x) = `(3x + 2)/(5x - 3)`. Then ______.
Let f : R → R be defind by f(x) = `1/"x" AA "x" in "R".` Then f is ____________.
Let g(x) = x2 – 4x – 5, then ____________.
The mapping f : N → N is given by f(n) = 1 + n2, n ∈ N when N is the set of natural numbers is ____________.
Let f : R `->` R be a function defined by f(x) = x3 + 4, then f is ______.
The function f: R → R defined as f(x) = x3 is:
A general election of Lok Sabha is a gigantic exercise. About 911 million people were eligible to vote and voter turnout was about 67%, the highest ever

Let I be the set of all citizens of India who were eligible to exercise their voting right in the general election held in 2019. A relation ‘R’ is defined on I as follows:
R = {(V1, V2) ∶ V1, V2 ∈ I and both use their voting right in the general election - 2019}
- Mr. ’X’ and his wife ‘W’ both exercised their voting right in the general election-2019, Which of the following is true?
Let the function f: R → R be defined by f(x) = 4x – 1, ∀ x ∈ R then 'f' is
Which one of the following graphs is a function of x?
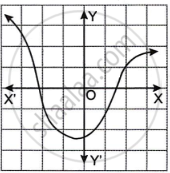 |
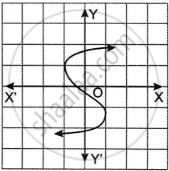 |
| Graph A | Graph B |
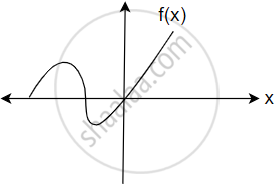
The given function f : R → R is not ‘onto’ function. Give reason.
