Advertisements
Advertisements
प्रश्न
The function f : R → R defined by
`f (x) = 2^x + 2^(|x|)` is
विकल्प
one-one and onto
many-one and onto
one-one and into
many-one and into
उत्तर
(d) many-one and into
Graph for the given function is as follows.
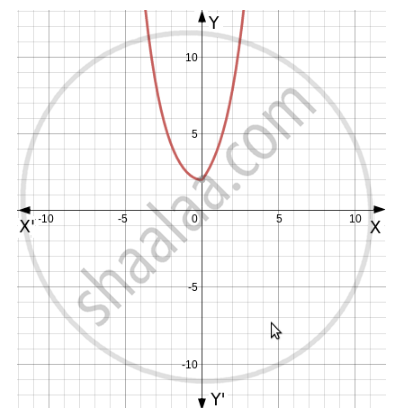
A line parallel to X axis is cutting the graph at two different values.
Therefore, for two different values of x we are getting the same value of y.
That means it is many one function.[2 , ∞ ) and R is the co-domain of the given function.
Hence, Co-domain ≠ Range Therefore, the given function is into.
APPEARS IN
संबंधित प्रश्न
Show that the function f in `A=R-{2/3} ` defined as `f(x)=(4x+3)/(6x-4)` is one-one and onto hence find f-1
Check the injectivity and surjectivity of the following function:
f: Z → Z given by f(x) = x3
Show that the Signum Function f: R → R, given by `f(x) = {(1, if x > 0), (0, if x = 0), (-1, if x < 0):}` is neither one-one nor onto
Give an example of a function which is not one-one but onto ?
Which of the following functions from A to B are one-one and onto?
f2 = {(2, a), (3, b), (4, c)} ; A = {2, 3, 4}, B = {a, b, c}
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = sin2x + cos2x
If A = {1, 2, 3}, show that a one-one function f : A → A must be onto.
If A = {1, 2, 3}, show that a onto function f : A → A must be one-one.
Suppose f1 and f2 are non-zero one-one functions from R to R. Is `f_1 / f^2` necessarily one - one? Justify your answer. Here,`f_1/f_2 : R → R is given by (f_1/f_2) (x) = (f_1(x))/(f_2 (x)) for all x in R .`
Given A = {2, 3, 4}, B = {2, 5, 6, 7}. Construct an example of each of the following:
(i) an injective map from A to B
(ii) a mapping from A to B which is not injective
(iii) a mapping from A to B.
Consider f : N → N, g : N → N and h : N → R defined as f(x) = 2x, g(y) = 3y + 4 and h(z) = sin z for all x, y, z ∈ N. Show that ho (gof) = (hog) of.
Find fog and gof if : f (x) = |x|, g (x) = sin x .
State with reason whether the following functions have inverse :
g : {5, 6, 7, 8} → {1, 2, 3, 4} with g = {(5, 4), (6, 3), (7, 4), (8, 2)}
Let f : R `{- 4/3} `- 43 →">→ R be a function defined as f(x) = `(4x)/(3x +4)` . Show that f : R - `{-4/3}`→ Rang (f) is one-one and onto. Hence, find f -1.
If f : R → (0, 2) defined by `f (x) =(e^x - e^(x))/(e^x +e^(-x))+1`is invertible , find f-1.
Which one of the following graphs represents a function?

If A = {1, 2, 3} and B = {a, b}, write the total number of functions from A to B.
If f : C → C is defined by f(x) = x2, write f−1 (−4). Here, C denotes the set of all complex numbers.
Let C denote the set of all complex numbers. A function f : C → C is defined by f(x) = x3. Write f−1(1).
Let \[f : \left( - \frac{\pi}{2}, \frac{\pi}{2} \right) \to R\] be a function defined by f(x) = cos [x]. Write range (f).
Write the domain of the real function f defined by f(x) = `sqrt (25 -x^2)` [NCERT EXEMPLAR]
Let\[A = \left\{ x \in R : - 1 \leq x \leq 1 \right\} = \text{B and C} = \left\{ x \in R : x \geq 0 \right\} and\]\[S = \left\{ \left( x, y \right) \in A \times B : x^2 + y^2 = 1 \right\} \text{and } S_0 = \left\{ \left( x, y \right) \in A \times C : x^2 + y^2 = 1 \right\}\]
Then,
\[f : A \to \text{B given by } 3^{ f\left( x \right)} + 2^{- x} = 4\] is a bijection, then
The function
Let [x] denote the greatest integer less than or equal to x. If \[f\left( x \right) = \sin^{- 1} x, g\left( x \right) = \left[ x^2 \right]\text{ and } h\left( x \right) = 2x, \frac{1}{2} \leq x \leq \frac{1}{\sqrt{2}}\]
Show that the function f: R → R defined by f(x) = `x/(x^2 + 1)`, ∀ ∈ + R , is neither one-one nor onto
Set A has 3 elements and the set B has 4 elements. Then the number of injective mappings that can be defined from A to B is ______.
Let X = {1, 2, 3}and Y = {4, 5}. Find whether the following subset of X ×Y are function from X to Y or not
h = {(1,4), (2, 5), (3, 5)}
Let A = [–1, 1]. Then, discuss whether the following functions defined on A are one-one, onto or bijective:
h(x) = x|x|
Let f: R → R be the functions defined by f(x) = x3 + 5. Then f–1(x) is ______.
The function f : R → R defined by f(x) = 3 – 4x is ____________.
If f: R → R given by f(x) =(3 − x3)1/3, find f0f(x)
Let f: R → R defined by f(x) = x4. Choose the correct answer
Number of integral values of x satisfying the inequality `(3/4)^(6x + 10 - x^2) < 27/64` is ______.
Let f(x) = ax (a > 0) be written as f(x) = f1(x) + f2(x), where f1(x) is an even function and f2(x) is an odd function. Then f1(x + y) + f1(x – y) equals ______.
If f : R `rightarrow` R is defined by `f(x) = (2x - 7)/4`, show that f(x) is one-one and onto.
